题目内容
13.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成如图图案.
则第8个图案中有25个白色菱形纸片;若第n个图案中有2017个白色纸片,则n的值为672.
分析 观察图形发现:白色纸片在4的基础上,依次多3个;根据其中的规律得出第n个图案中有白色纸片,求出n=8、n=2017的值即可.
解答 解:∵第1个图案中有白色纸片3×1+1=4张
第2个图案中有白色纸片3×2+1=7张,
第3图案中有白色纸片3×3+1=10张,
∴第n个图案中有白色纸片3n+1张,
当n=8时,3n+1=25
当n=8时,3n+1=672,
故答案为:25,672.
点评 此题主要考查图形的变化规律,此题的关键是注意发现前后图形中的数量之间的关系.

练习册系列答案
相关题目
3.顺次连结四边形四条边的中点,所得的四边形是矩形,则原四边形一定是( )
| A. | 平行四边形 | B. | 对角线相等的四边形 | ||
| C. | 对角线互相垂直的四边形 | D. | 矩形 |
4.下列说法正确地有( )
(1)点(1,-a)一定在第四象限 (2)坐标轴上的点不属于任一象限 (3)若点(a,b)在坐标轴的角平分线上,则a=b (4)直角坐标系中,在y轴上且到原点的距离为5的点的坐标是(0,5)
(1)点(1,-a)一定在第四象限 (2)坐标轴上的点不属于任一象限 (3)若点(a,b)在坐标轴的角平分线上,则a=b (4)直角坐标系中,在y轴上且到原点的距离为5的点的坐标是(0,5)
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.以下列各组线段为边,能组成三角形的是( )
| A. | 2,2,4 | B. | 2,3,6 | C. | 1,2,3 | D. | 3,4,5 |
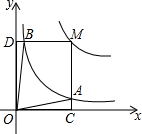 反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.
反比例函数y=$\frac{a}{x}$(a>0,a为常数)和y=$\frac{2}{x}$在第一象限内的图象如图所示,点M在y=$\frac{a}{x}$的图象上,MC⊥x轴于点C,交y=$\frac{2}{x}$的图象于点A;MD⊥y轴于点D,交y=$\frac{2}{x}$的图象于点B,当点M在y=$\frac{a}{x}$的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是①②③.