题目内容
5.化简:$\sqrt{12}$=2$\sqrt{3}$,-$\sqrt{4\frac{1}{4}}$=-$\frac{\sqrt{17}}{2}$,$\sqrt{\frac{2}{3a}}$=$\frac{\sqrt{6a}}{3a}$.分析 利用积的算术平方根的性质化简$\sqrt{12}$,利用商的算术平方根的性质化简-$\sqrt{4\frac{1}{4}}$,$\sqrt{\frac{2}{3a}}$.
解答 解:$\sqrt{12}$=$\sqrt{4×3}$=2$\sqrt{3}$,
-$\sqrt{4\frac{1}{4}}$=-$\sqrt{\frac{17}{4}}$=-$\frac{\sqrt{17}}{2}$,
$\sqrt{\frac{2}{3a}}$=$\sqrt{\frac{2•3a}{3a•3a}}$=$\frac{\sqrt{6a}}{3a}$.
故答案为2$\sqrt{3}$,-$\frac{\sqrt{17}}{2}$,$\frac{\sqrt{6a}}{3a}$.
点评 本题考查了二次根式的性质与化简,掌握积的算术平方根的性质和商的算术平方根的性质是解题的关键.化简二次根式的步骤:①把被开方数分解因式;②利用积的算术平方根的性质,把被开方数中能开得尽方的因数(或因式)都开出来;③化简后的二次根式中的被开方数中每一个因数(或因式)的指数都小于根指数2.

练习册系列答案
相关题目
15.若|a-3|+$\sqrt{2+b}$=0,则a+b的值是( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |

 如图,将△ABC沿BC方向平移3cm得到△DEF,如果四边形ABFD的周长是28cm,则△ABC的周长是22cm.
如图,将△ABC沿BC方向平移3cm得到△DEF,如果四边形ABFD的周长是28cm,则△ABC的周长是22cm.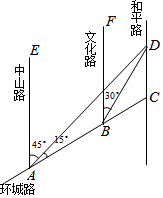 如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C,经测量,花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.
如图,AC是某市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C,经测量,花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=2km,∠DAC=15°.