题目内容
14.设x1,x2是关于x的方程x2+(m-1)x-m=0(m≠0)的两个根,且满足$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=-$\frac{2}{3}$,求m的值.分析 根据根与系数的关系可得出x1+x2=1-m、x1•x2=-m,将$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$通分后代入数据即可得出关于m的分式方程,解之即可得出m的值.
解答 解:∵x1,x2是关于x的方程x2+(m-1)x-m=0(m≠0)的两个根,
∴x1+x2=1-m,x1•x2=-m,
∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{1-m}{-m}$=-$\frac{2}{3}$,
解得:m=$\frac{3}{5}$,
经检验m=$\frac{3}{5}$是方程$\frac{1-m}{-m}$=-$\frac{2}{3}$的解.
点评 本题考查了根与系数的关系,熟练掌握“x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$”是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
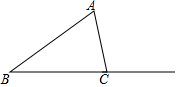 在证明三角形内角和定理时,小明的想法是把三个角凑到C处,他过点C作直线CD∥AB,请你按照他的想法在图中作出直线CD.
在证明三角形内角和定理时,小明的想法是把三个角凑到C处,他过点C作直线CD∥AB,请你按照他的想法在图中作出直线CD.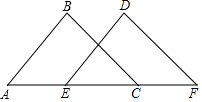 如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.求证:∠B=∠D.
如图,A,E,C,F在同一条直线上,AB=FD,BC=DE,AE=FC.求证:∠B=∠D.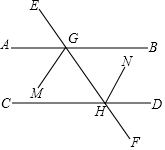 如图,AB∥CD,MG平分∠AGF,NH平分∠EHD,那么GM∥HN,请说明理由.
如图,AB∥CD,MG平分∠AGF,NH平分∠EHD,那么GM∥HN,请说明理由. 列方程解应用题:
列方程解应用题: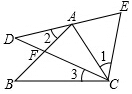 如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于AB(请用图形中的线段表示)
如图,A在DE上,F在AB上,且AC=CE,∠1=∠2=∠3,则DE的长等于AB(请用图形中的线段表示)