题目内容
定义符号“*”表示的运算法则为a*b=ab+3a,若(3*x)+(x*3)=-27,则x=
A. 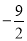 B.
B. 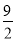 C. 4 D. -4
C. 4 D. -4
练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
题目内容
定义符号“*”表示的运算法则为a*b=ab+3a,若(3*x)+(x*3)=-27,则x=
A. 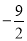 B.
B. 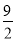 C. 4 D. -4
C. 4 D. -4
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案