��Ŀ����
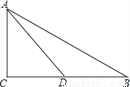
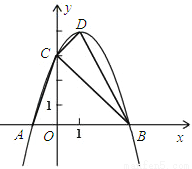
��ͼ����֪������y=- x2+bx+c��x�ύ�ڵ�A��-1��0����B����y�ύ�ڵ�C��0��3����
(1)��������ߵĽ���ʽ����B�����ꣻ
(2)�������ߵĶ���ΪD������CD��DB��CB��AC��
����֤����AOC�ס�DCB���������������Ƿ������ԭ��O���غϵĵ�P��ʹ��P��A��CΪ��������������DCB���ƣ������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
��ϰ��ϵ�д�
�����Ŀ


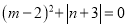 ����
����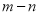 ������ƽ������__________.
������ƽ������__________.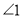 ��
��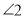 �ǶԶ��ǣ���ô
�ǶԶ��ǣ���ô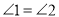 ���������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�����
���������ε�һ����Ǵ����κ�һ�����������ڵ��ڽǣ�����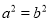 ����
����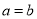 .
.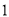 �� B.
�� B. 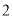 �� C.
�� C. 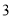 �� D.
�� D. 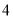 ��
��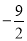 B.
B. 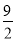 C. 4 D. ��4
C. 4 D. ��4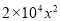 ��ϵ����2
��ϵ����2