题目内容
9.计算:(1)(-$\frac{1}{2}$)4÷(-2)-3÷2-2;
(2)$\frac{2x+1}{x+1}$$÷\frac{1-4{x}^{2}}{1-{x}^{2}}$$•\frac{1}{x-1}$;
(3)($\frac{{x}^{2}-{y}^{2}}{xy}$)2÷(x+y)•($\frac{x}{x-y}$)3;
(4)$\frac{x-y}{x+3y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}+6xy+9{y}^{2}}$-$\frac{2y}{x+y}$.
分析 (1)先根据负整数指数幂及有理数乘方的法则分别计算出各数,再从左到右依次计算即可;
(2)从左到右依次计算即可;
(3)先算乘方,再算乘除即可;
(4)先算除法,再算减法即可.
解答 解:(1)原式=$\frac{1}{16}$×(-8)×4
=-2;
(2)原式=$\frac{2x+1}{x+1}$•$\frac{(x+1)(x-1)}{(2x-1)(1+2x)}$•$\frac{1}{x-1}$
=$\frac{x-1}{2x-1}$•$\frac{1}{x-1}$
=$\frac{1}{2x-1}$;
(3)原式=$\frac{(x+y)^{2}(x-y)^{2}}{{x}^{2}{y}^{2}}$•$\frac{1}{x+y}$•$\frac{{x}^{3}}{(x-y)^{3}}$
=$\frac{{(x+y)}^{\;}{(x-y)}^{2}}{{x}^{2}{y}^{2}}$•$\frac{{x}^{3}}{{(x-y)}^{3}}$
=$\frac{x+y}{x(x-y)}$;
(4)原式=$\frac{x-y}{x+3y}$•$\frac{(x+3y)^{2}}{(x+y)(x-y)}$-$\frac{2y}{x+y}$
=$\frac{x+3y}{x+y}$-$\frac{2y}{x+y}$
=$\frac{x+y}{x+y}$
=1.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
14.已知x=1$\underset{\underbrace{00…0}}{n个0}$01$\underset{\underbrace{00…0}}{n+1个0}$50,则( )
| A. | x是完全平方数 | B. | x-25是完全平方数 | ||
| C. | x-50是完全平方数 | D. | x+50是完全平方数 |
17.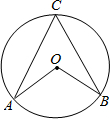 如图,∠ACB和∠AOB是⊙0中弧AB所对的圆周角和圆心角,∠AOB=80°,则弧AB所对圆周角的度数是( )
如图,∠ACB和∠AOB是⊙0中弧AB所对的圆周角和圆心角,∠AOB=80°,则弧AB所对圆周角的度数是( )
 如图,∠ACB和∠AOB是⊙0中弧AB所对的圆周角和圆心角,∠AOB=80°,则弧AB所对圆周角的度数是( )
如图,∠ACB和∠AOB是⊙0中弧AB所对的圆周角和圆心角,∠AOB=80°,则弧AB所对圆周角的度数是( )| A. | 40° | B. | 45° | C. | 50° | D. | 80° |
 在筝形ABCD中,AD=CD,AB=BC,若∠ADC=∠ABC,∠DAC=45°,求证:筝形ABCD是正方形.
在筝形ABCD中,AD=CD,AB=BC,若∠ADC=∠ABC,∠DAC=45°,求证:筝形ABCD是正方形. 某空中加油机接到命令,立即给一架正在飞行的运输机进行空中加油,在加油过程中,设运输机机油箱的余油量为Q1吨,加油机的加油邮箱余油量为Q2吨,加油时间为t分钟,Q1,Q2与t之间的关系如图所示,结合图象回答问题:加油机的加油油箱中装载了多少吨油?将这些油全部加给运输机需要多少分钟?
某空中加油机接到命令,立即给一架正在飞行的运输机进行空中加油,在加油过程中,设运输机机油箱的余油量为Q1吨,加油机的加油邮箱余油量为Q2吨,加油时间为t分钟,Q1,Q2与t之间的关系如图所示,结合图象回答问题:加油机的加油油箱中装载了多少吨油?将这些油全部加给运输机需要多少分钟? 如图,矩形ABCD的对角线AC,BD相交于点O,∠COB=2∠BOA,对角线AC=10cm,求AB的长.
如图,矩形ABCD的对角线AC,BD相交于点O,∠COB=2∠BOA,对角线AC=10cm,求AB的长.