题目内容
16．先化简$\frac{2x-4}{{x}^{2}-1}$÷$\frac{x-2}{{x}^{2}+2x+1}$-$\frac{2x}{x-1}$，再求值，其中x=2$\sqrt{2}$+3．分析 原式第一项利用除法法则变形，约分后利用同分母分式的减法法则计算得到最简结果，把x的值代入计算即可求出值．
解答 解：原式=$\frac{2（x-2）}{（x+1）（x-1）}$•$\frac{（x+1）^{2}}{x-2}$-$\frac{2x}{x-1}$=$\frac{2（x+1）}{x-1}$-$\frac{2x}{x-1}$=$\frac{2}{x-1}$，
当x=2$\sqrt{2}$+3时，原式=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
如图，△ABC中，点D，E，F分别是BC，AD，CE的中点，S△ABC=12，则S△DEF=1.5．
将直角三角尺的顶点靠在直尺上，且斜边与这根直尺平行，那么在形成的这个图中（如图），与∠α互余的角共有2个．
如图，四边形ABCD是平行四边形，以AB为直径的⊙0经过点D，E是⊙O上一点，且∠AED=45°，
5．计算（-$\frac{4}{5}$）15×（1.25）14的结果是（ ）
| A． | -$\frac{4}{5}$ | B． | $\frac{4}{5}$ | C． | $\frac{5}{4}$ | D． | -$\frac{5}{4}$ |
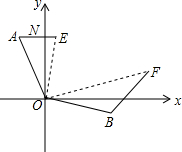如图，在一次海关缉私行动中，发现一走私艇在海关指挥艇（O处）北偏西30°的A处，此时缉私艇在指挥艇南偏东70°的B处，并且两船到指挥艇的距离相等，现发现走私艇向正东方向以30海里/小时的速度前进，与此同时缉私艇沿北偏东50°的方向以40海里/小时的速度前进1小时后，指挥艇观测走私艇，缉私艇分别到达E，F处，这时两船的夹角∠EOF=70°，试求此时两船之间的距离．