题目内容
6.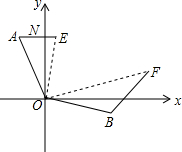 如图,在一次海关缉私行动中,发现一走私艇在海关指挥艇(O处)北偏西30°的A处,此时缉私艇在指挥艇南偏东70°的B处,并且两船到指挥艇的距离相等,现发现走私艇向正东方向以30海里/小时的速度前进,与此同时缉私艇沿北偏东50°的方向以40海里/小时的速度前进1小时后,指挥艇观测走私艇,缉私艇分别到达E,F处,这时两船的夹角∠EOF=70°,试求此时两船之间的距离.
如图,在一次海关缉私行动中,发现一走私艇在海关指挥艇(O处)北偏西30°的A处,此时缉私艇在指挥艇南偏东70°的B处,并且两船到指挥艇的距离相等,现发现走私艇向正东方向以30海里/小时的速度前进,与此同时缉私艇沿北偏东50°的方向以40海里/小时的速度前进1小时后,指挥艇观测走私艇,缉私艇分别到达E,F处,这时两船的夹角∠EOF=70°,试求此时两船之间的距离.
分析 连接EF,延长FB到G,使BG=AE,连接OG,根据同角的补角相等求出∠OAE=∠OBG,然后利用“边角边”证明△AOE和△BOG全等,根据全等三角形对应边相等可得OE=OG,∠AOE=∠BOG,再求出∠EOF=∠GOF,然后利用“边角边”证明△OEF和△OGF全等,根据全等三角形对应边相等可得EF=GF,然后得出EF=AE+BF.
解答 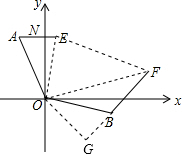 解:如图,连接EF,延长FB到G,使BG=AE,连接OG.
解:如图,连接EF,延长FB到G,使BG=AE,连接OG.
∵∠OAE+∠OBF=(90°-30°)+(70°+50°)=180°,∠OBG+∠OBF=180°,
∴∠OAE=∠OBG,
在△AOE和△BOG中,
$\left\{\begin{array}{l}{OA=OB}\\{∠OAE=∠OBG}\\{AE=BG}\end{array}\right.$,
∴△AOE≌△BOG(SAS),
∴OE=OG,∠AOE=∠BOG,
∵∠EOF=70°,∠AOB=30°+90°+(90°-70°)=140°,
∴∠GOF=∠BOG+∠BOF=∠AOE+∠BOF=∠AOB-∠EOF=70°=∠EOF,
∴∠EOF=∠GOF.
在△OEF和△OGF中,
$\left\{\begin{array}{l}{OE=OG}\\{∠EOF=∠GOF}\\{OF=OF}\end{array}\right.$,
∴△OEF≌△OGF(SAS),
∴EF=GF,
∵GF=BG+BF=AE+BF,
∴EF=AE+BF,即EF=1×(30+40)=70海里.
答:此时两舰艇之间的距离是70海里.
点评 本题考查了解直角三角形的应用-方向角问题,全等三角形的判定与性质,作辅助线构造出全等三角形并两次证明三角形全等是解题的关键,也是本题的难点.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
11.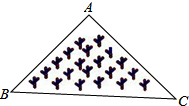 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )| A. | △ABC的三条中线的交点 | B. | △ABC三条角平分线的交点 | ||
| C. | △ABC三条高所在直线的交点 | D. | △ABC三边的中垂线的交点 |
18.若非零实数m,n满足m(m-4n)=0,则分式$\frac{{{m^2}+1}}{{{m^2}-2mn}}-\frac{1}{2mn}$的值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $\frac{1}{3}$ |
16.下列各组数的大小比较中,正确的是( )
| A. | 1>2 | B. | -3>-2 | C. | 0>-1 | D. | $\sqrt{2}$>2 |