题目内容
1.已知Rt△ABC,∠C=90°,AB=13,AC=12,以AC所在直线为轴,将此三角形旋转1周,所得圆锥的侧面积是65π.
分析 首先确定圆锥的母线长和圆锥的底面半径,利用侧面积计算公式直接求得圆锥的侧面积即可.
解答 解:∵∠C=90°,AB=13,AC=12,
∴BC=5,
以AC所在直线为轴旋转一周,所得圆锥的底面周长=10π,侧面积=$\frac{1}{2}$×10π×13=65π,
故答案为:65π.
点评 考查了圆锥的计算,正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键,理解圆锥的母线长是扇形的半径,圆锥的底面圆周长是扇形的弧长.

练习册系列答案
相关题目
11.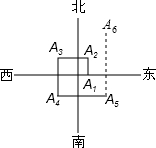 如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
 如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )
如图,一个机器人从O点出发,向正东方向走3m,到达A1点,再向正北走6m到达A2点,再向正西走9m到达A3点,再向正南走12m,到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,当机器人走到A6点时,A6点的坐标是( )| A. | (9,12) | B. | (9,9) | C. | (9,6) | D. | (9,3) |
12.若关于x的分式方程$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$无解,则m的值为( )
| A. | -l.5 | B. | 1 | C. | -l.5或2 | D. | -0.5或-l.5 |
9.下列各数能用科学记数法表示为3.14×10-3的是( )
| A. | 0.000314 | B. | 0.00314 | C. | 0.0314 | D. | 3140 |
6.学校举行数学知识竞赛,设立了一、二、三等奖,计划共购买45件奖品,其中二等奖奖品件数比一等奖奖品件数的2倍还少5件,已知购买一等奖奖品x件.各种奖品的单价如下表:
(1)学校购买二等奖奖品2x-5件,三等奖奖品50-3x件;(用含x的代数式表示)
(2)若购买三等奖奖品的费用不超过二等奖奖品的费用的2倍,学校为节省开支,应如何购买这三种奖品?总费用最少是多少元?
| 奖品 | 一等奖奖品 | 二等奖奖品 | 三等奖奖品 |
| 单价(元) | 12 | 10 | 8 |
(2)若购买三等奖奖品的费用不超过二等奖奖品的费用的2倍,学校为节省开支,应如何购买这三种奖品?总费用最少是多少元?
13.苏北五市联合通过网络投票选出了一批“最有孝心的美少年”.根据各市的入选结果制作出如下统计表,后来发现,统计表中前三行的所有数据都是正确的,后两行中有一个数据是错误的.请回答下列问题:
(1)统计表a=0.1,b=8;
(2)统计表后三行中哪一个数据是错误的?该数据的正确值是多少?
(3)组委会决定从来自宿迁市的4位“最有孝心的美少年”中,任选两位作为苏北五市形象代言人,A、B是宿迁市“最有孝心的美少年”中的两位,问A、B同时入选的概率是多少?并请画出树状图或列出表格.
(1)统计表a=0.1,b=8;
(2)统计表后三行中哪一个数据是错误的?该数据的正确值是多少?
(3)组委会决定从来自宿迁市的4位“最有孝心的美少年”中,任选两位作为苏北五市形象代言人,A、B是宿迁市“最有孝心的美少年”中的两位,问A、B同时入选的概率是多少?并请画出树状图或列出表格.
| 区域 | 频数 | 频率 |
| 宿迁 | 4 | A |
| 连云港 | 7 | 0.175 |
| 淮安 | b | 0.2 |
| 徐州 | 10 | 0.25 |
| 盐城 | 12 | 0.275 |
10.方程与下列哪个方程组合,使得方程组的解是$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$( )
| A. | 3x+2y=7 | B. | -2x+y=-3 | C. | 6x+y=8 | D. | 以上都不对 |
11.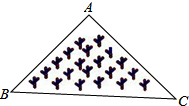 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )| A. | △ABC的三条中线的交点 | B. | △ABC三条角平分线的交点 | ||
| C. | △ABC三条高所在直线的交点 | D. | △ABC三边的中垂线的交点 |