题目内容
7. 如图,△ABC中,点D,E,F分别是BC,AD,CE的中点,S△ABC=12,则S△DEF=1.5.
如图,△ABC中,点D,E,F分别是BC,AD,CE的中点,S△ABC=12,则S△DEF=1.5.
分析 根据三角形的中线把三角形分成两个面积相等的三角形,分别求出三角形ACD、CDE、DEF的面积各是多少即可.
解答 解:∵点D是BC的中点,
∴S△ACD=$\frac{1}{2}$S△ABC=$\frac{1}{2}×12$=6;
∵点E是AD的中点,
∴S△CDE=$\frac{1}{2}$S△ACD=$\frac{1}{2}×$6=3;
∵点F是CE的中点,
∴S△DEF=$\frac{1}{2}$S△CDE=$\frac{1}{2}×$3=1.5.
故答案为:1.5.
点评 此题主要考查了三角形的面积的求法,解答此题的关键是要明确:三角形的中线把三角形分成两个面积相等的三角形.

练习册系列答案
相关题目
12.若关于x的分式方程$\frac{2m+x}{x-3}$-1=$\frac{2}{x}$无解,则m的值为( )
| A. | -l.5 | B. | 1 | C. | -l.5或2 | D. | -0.5或-l.5 |
19.下列各式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{3}$-1 | B. | $\sqrt{6}$ | C. | $\sqrt{9}$ | D. | $\sqrt{12}$ |
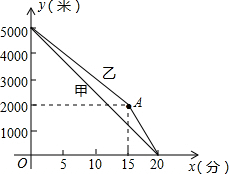 甲乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数的图象如图所示,根据图象所提供的信息解答下列问题:
甲乙两名运动员进行长跑训练,两人距终点的路程y(米)与跑步时间x(分)之间的函数的图象如图所示,根据图象所提供的信息解答下列问题: