题目内容
11.某学校为了解八年级学生的课外阅读情况,钟老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示,但不完整的统计图,根据图示信息,解答下列问题: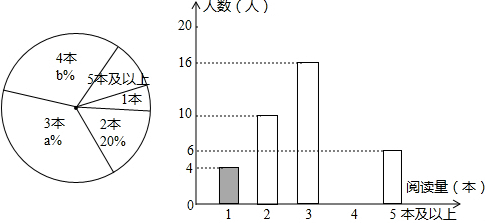
(1)求被抽查学生人数及课外阅读量的众数;
(2)求扇形统计图中的a、b值;
(3)将条形统计图补充完整.
分析 (1)利用被抽查学生人数=读2本的人数÷对应的百分比,课外阅读量的众数是3;
(2)分别求出它们的百分数,即可得出a,b的值;
(3)先求出阅读量为4本的人数,再补全统计图即可.
解答 解:(1)10÷20%=50(人),课外阅读量的众数是3;
(2)a%=$\frac{16}{50}$×100%=32%,b%=$\frac{50-4-10-16-6}{50}$×100%=28%,
∴a=32,b=28;
(3)如图,阅读量为4本的人数为:50-4-10-16-6=14(人).
点评 本题主要考查了条形统计图,扇形统计图及众数,解题的关键是读懂统计图,能从统计图中获得准确的信息.

练习册系列答案
相关题目
2.下列各数等于3的是( )
| A. | -$\sqrt{{3}^{2}}$ | B. | -$\sqrt{(-3)^{2}}$ | C. | (-$\sqrt{\frac{1}{3}}$)2 | D. | $\sqrt{(-\frac{1}{3})^{-2}}$ |
16. 如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )
如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )
 如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )
如图,双曲线y=$\frac{4}{x}$与正比例函数y=kx的图象交于A,B两点,过点A作AC⊥y轴于点C,连接BC,则△ABC的面积为( )| A. | 2 | B. | $\frac{1}{2}$ | C. | 4 | D. | $\frac{1}{4}$ |
20.已知a<b,二次根式$\sqrt{-{a}^{3}b}$化简为( )
| A. | a$\sqrt{ab}$ | B. | a$\sqrt{-ab}$ | C. | -a$\sqrt{ab}$ | D. | -a$\sqrt{-ab}$ |
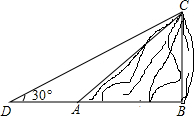 如图,某人在D处测得山顶C的仰角为30°,向前走30米到达山脚A处,测得山坡AC的坡度为i=1:1.5,求山顶的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数).
如图,某人在D处测得山顶C的仰角为30°,向前走30米到达山脚A处,测得山坡AC的坡度为i=1:1.5,求山顶的高度(不计测角仪的高度,$\sqrt{3}$≈1.73,结果保留整数). 已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A(-1,4)和B(2,m)两点,试确定双曲线和直线的函数关系式.
已知双曲线y=$\frac{k}{x}$和直线y=ax+b相交于A(-1,4)和B(2,m)两点,试确定双曲线和直线的函数关系式.