题目内容
15.某公司有甲、乙两个绿色农产品种植基地,在收获期这两个基地当天收获的某种农产品,一部份存入仓库,另一部分运往外地销售.根据经验,该农产品在收获过程中两个种植基地累积总产量y(吨)与收获天数x(天)满足函数关系y=2x+3(其中1≤x≤10且x为整数).该农产品在收获过程中甲、乙两基地的累积产量分别占两基地累积总产量的百分比和甲、乙两基地累积存入仓库的量分别占甲、乙两基地的累积产量的百分比如下表:| 种植基地 | 该基地的累积产量占两 基地累积总产量的百分比 | 该基地累积存入仓库的量占 该基地的累积产量的百分比 |
| 甲基地 | 60% | 85% |
| 乙基地 | 40% | 22.5% |
(2)设在收获过程中甲、乙两基地累积存入仓库的该种农产品的总量为p(吨),请求出p(吨)与收获天数x(天)的函数关系式;
(3)在(2)的基础上,若仓库内原有该农产品42.6吨,为满足本地市场需求,在此收获期开始的同时,每天从仓库调出一部分该种农产品投入本地市场,若在本地市场售出的该种农产品总量m(吨)与收获天数x(天)满足函数关系m=-x2+13.2x-1.6(1≤x≤10且x为整数).问在此收获期内连续销售几天,该农产品库存量达到最低值?最低库存量是多少吨?
分析 (1)根据等量关系“该地累积存入仓库中的量=累积产量分别占两基地累积总产量的百分比×累积存入仓库的量占累积产量的百分比×累积总产量”通过表中的数据用y表示出甲乙两基地累积存入仓库中的量;
(2)根据等量关系“存入仓库的该种农产品总产量=甲基地存入仓库的总产量+乙基地存入仓库的总产量”列出函数关系式;
(3)根据等量关系“该产品库存量=原存入量+收获时存入量-售出量”列出函数关系式并求得最小值.
解答 解:(1)①甲基地累积存入仓库的量:
85%×60%y=0.51y(吨).
②乙基地累积存入仓库的量:
22.5%×40%y=0.09y(吨).
(2)p=0.51y+0.09y=0.6y,
∵y=2x+3,
∴p=0.6(2x+3)=1.2x+1.8.
(3)设在此收获期内仓库库存该种农产品T吨.
T=42.6+p-m
=42.6+1.2x+1.8-(-x2+13.2x-1.6)
=x2-12x+46=(x-6)2+10,
∵1>0,
∴抛物线的开口向上,
又∵1≤x≤10且x为整数,
∴当x=6时,T的最小值为10;
∴在此收获期内连续销售6天,该农产品库存达最低值,最低库存为10吨.
点评 本题主要考查了列函数表达式和运用二次函数的性质求实际问题最值,审清题意正确列出函数表达式是解决问题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
10.在△ABC中,∠C=90°,BC:AC=1:2,则cosA=( )
| A. | 2 | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
20.下列比较大小正确的是( )
| A. | $\root{3}{6}$<1 | B. | $\root{3}{-8}$=$\root{3}{8}$ | C. | $\sqrt{15}$>4 | D. | $\sqrt{3}$-2>-$\frac{\sqrt{3}}{2}$ |
7.在“百度”搜索引擎中输入“雾霾天气形成的原因”,搜索的相关结果约为6430000,将数字6430000用科学记数法表示为( )
| A. | 6.43×105 | B. | 0.643×107 | C. | 64.3×105 | D. | 6.43×106 |
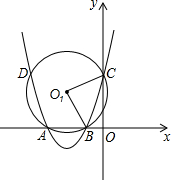 如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.
如图,抛物线y=ax2+bx+3过点A(-3,0),B(-1,0),与y轴相交于点C,⊙O1经过A,B,C三点,与抛物线相交于另一点D.
 如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则AE:EC=$\sqrt{2}$+1.
如图,平行于BC的直线DE把△ABC分成的两部分面积相等,则AE:EC=$\sqrt{2}$+1.