题目内容
15. 如图,点B、E、C、F在同一直线上,BE=CF,∠B=∠F,再添加一个条件仍不能证明△ABC≌△DFE的是( )
如图,点B、E、C、F在同一直线上,BE=CF,∠B=∠F,再添加一个条件仍不能证明△ABC≌△DFE的是( )| A. | AB=DF | B. | ∠A=∠D | C. | AC∥DE | D. | AC=DE |
分析 根据全等三角形的判定定理进行解答.
解答 解:由BE=CF得到:BC=FE.
A、由条件BC=FE,∠B=∠F添加AB=DF,根据全等三角形的判定定理SAS能证明△ABC≌△DFE,故本选项错误;
B、由条件BC=FE,∠B=∠F添加∠A=∠D,根据全等三角形的判定定理AAS能证明△ABC≌△DFE,故本选项错误;
C、因为AC∥DE,所以∠ACB=∠DEF,再由条件BC=FE,∠B=∠F,根据全等三角形的判定定理ASA能证明△ABC≌△DFE,故本选项错误;
D、由条件BC=FE,∠B=∠F添加AC=DE,由SSA不能证明△ABC≌△DFE,故本选项正确.
故选:D.
点评 本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
相关题目
5.某铁路因大雨导致严重破坏,为抢修其中一段150米的铁路,施工队每天比原计划多修5米,结果提前3天开通了列车.问原计划每天修多少米?若原计划每天修x米,所列方程正确的是( )
| A. | $\frac{150}{x}$-$\frac{150}{x+5}$=3 | B. | $\frac{150}{x}$-$\frac{150}{x-5}$=3 | C. | $\frac{150}{x-5}$-$\frac{150}{x}$=3 | D. | $\frac{150}{x+5}$-$\frac{150}{x}$=3 |
6. 如图,在△ABC中,∠A=40°,∠C=70°,BD平分∠ABC,交AC于点D,则∠ABD的度数是( )
如图,在△ABC中,∠A=40°,∠C=70°,BD平分∠ABC,交AC于点D,则∠ABD的度数是( )
 如图,在△ABC中,∠A=40°,∠C=70°,BD平分∠ABC,交AC于点D,则∠ABD的度数是( )
如图,在△ABC中,∠A=40°,∠C=70°,BD平分∠ABC,交AC于点D,则∠ABD的度数是( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
3.在下列各数2π,5,-$\sqrt{4}$,6.1010010001…(每两个1之间多一个0),$\frac{131}{11}$,3.14159,$\sqrt{3}$中无理数的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.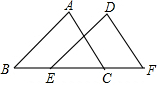 如图所示,△DEF是由△ABC经过平移得到的,则平移的距离可能是( )
如图所示,△DEF是由△ABC经过平移得到的,则平移的距离可能是( )
 如图所示,△DEF是由△ABC经过平移得到的,则平移的距离可能是( )
如图所示,△DEF是由△ABC经过平移得到的,则平移的距离可能是( )| A. | 线段BC的长度 | B. | 线段EC的长度 | C. | 线段BE的长度 | D. | 线段BF的长度 |
20.二次函数y=2x2-1的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )
| A. | 抛物线开口向下 | B. | 抛物线的对称轴是直线x=1 | ||
| C. | 抛物线经过点(2,1) | D. | 抛物线与x轴有两个交点 |
4. 下列A、B、C、D四个图中,能通过图M平移得到的是( )
下列A、B、C、D四个图中,能通过图M平移得到的是( )
 下列A、B、C、D四个图中,能通过图M平移得到的是( )
下列A、B、C、D四个图中,能通过图M平移得到的是( )| A. |  | B. |  | C. |  | D. |  |