题目内容
20.二次函数y=2x2-1的图象是一条抛物线,下列关于该抛物线的说法,正确的是( )| A. | 抛物线开口向下 | B. | 抛物线的对称轴是直线x=1 | ||
| C. | 抛物线经过点(2,1) | D. | 抛物线与x轴有两个交点 |
分析 根据二次函数的性质对A、B进行判断;根据二次函数图象上点的坐标特征对C进行判断;利用方程2x2-1=0解的情况对D进行判断.
解答 解:A、a=2,则抛物线y=2x2-1的开口向上,所以A选项错误;
B、抛物线的对称轴为直线x=0,所以B选项错误;
C、当x=2时,y=2×4-1=7,则抛物线不经过点(2,1),所以C选项错误;
D、当y=0时,2x2-1=0,此方程有两个不相等的实数解,所以D选项正确.
故选D.
点评 本题考查了二次函数的性质,主要涉及开口方向,对称轴,与y轴的交点坐标,最值问题,熟记二次函数的性质是解题的关键.

练习册系列答案
相关题目
10.正比例函数y=kx的图象经过点(1,-2),则该函数的图象经过的象限是( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
8.下列各式成立的是( )
| A. | 2$\sqrt{3}-\sqrt{3}$=2 | B. | $\sqrt{6}-\sqrt{3}$=3 | C. | ${(-\sqrt{\frac{2}{3}})^2}=-\frac{2}{3}$ | D. | $\sqrt{{{(-3)}^2}}$=3 |
15. 如图,点B、E、C、F在同一直线上,BE=CF,∠B=∠F,再添加一个条件仍不能证明△ABC≌△DFE的是( )
如图,点B、E、C、F在同一直线上,BE=CF,∠B=∠F,再添加一个条件仍不能证明△ABC≌△DFE的是( )
 如图,点B、E、C、F在同一直线上,BE=CF,∠B=∠F,再添加一个条件仍不能证明△ABC≌△DFE的是( )
如图,点B、E、C、F在同一直线上,BE=CF,∠B=∠F,再添加一个条件仍不能证明△ABC≌△DFE的是( )| A. | AB=DF | B. | ∠A=∠D | C. | AC∥DE | D. | AC=DE |
5.在直角坐标系内,将点P(1,-2)向左平移2个单位长度,再向上平移3个单位长度,可以得到对应点P1的坐标为( )
| A. | (-1,1) | B. | (-1,-5) | C. | (3,1) | D. | (3,-5) |
12.下列事件中,属于必然事件的是( )
| A. | 射击运动员射击一次,命中9环 | |
| B. | 掷一枚普通的正方体骰子,向上的一面出现的点数大于6 | |
| C. | 在同一年出生的13名学生中,至少有2人出生在同一个月 | |
| D. | 买一张电影票,座位号是偶数号 |
9.下列各式中一定是二次根式的是( )
| A. | $\sqrt{x+2}$ | B. | $\sqrt{x}$ | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{\frac{a}{2b}}$ |
10.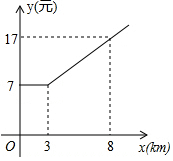 某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
 某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )| A. | 1.5元 | B. | 2元 | C. | 2.12元 | D. | 2.4元 |
 如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=3,AB的垂直平分线分别交AB于E,交BC于D,连接AD,则DE的长为1.
如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=3,AB的垂直平分线分别交AB于E,交BC于D,连接AD,则DE的长为1.