题目内容
7.如图,正方形纸片ABCD的边长为$\sqrt{2}$,对角线相交于点O,第一次将纸片折叠,使点A与点O重合,折痕与AO交于点P1;设P1O的中点为O1,第2次将纸片折叠,使点A与点O1重合,折痕与AO交于点P2;设P2O1的中点为O2,第3次将纸片折叠,使点A与点O2重合,折痕与AO交于点P3;…;设Pn-1On-2的中点为On-1,第n次将纸片折叠,使点A与On-1重合,折痕与AO交于点Pn(n>2),则APn的长为$\frac{1}{2}$×($\frac{3}{4}$)n-1.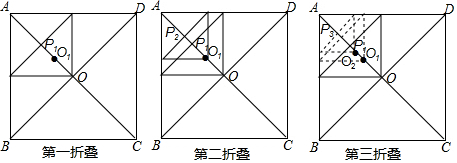
分析 先根据正方形的性质得到AO的长,再根据折叠的性质,依次得出AP1=$\frac{1}{2}$×($\frac{3}{4}$)1-1;AP2=$\frac{1}{2}$×($\frac{3}{4}$)2-1;AP3=$\frac{1}{2}$×($\frac{3}{4}$)3-1;据此可得规律APn=$\frac{1}{2}$×($\frac{3}{4}$)n-1.
解答  解:∵正方形纸片ABCD的边长为$\sqrt{2}$,对角线相交于点O,
解:∵正方形纸片ABCD的边长为$\sqrt{2}$,对角线相交于点O,
∴AO=$\frac{1}{2}$AC=$\frac{1}{2}$×2=1,
由题可得:
AP1=P1O=$\frac{1}{2}$AO=$\frac{1}{2}$=$\frac{1}{2}$×($\frac{3}{4}$)1-1;
∵P1O1=O1O=$\frac{1}{2}$P1O=$\frac{1}{4}$,
∴AO1=AO-O1O=1-$\frac{1}{4}$=$\frac{3}{4}$,
∴AP2=P2O1=$\frac{1}{2}$AO1=$\frac{1}{2}$×$\frac{3}{4}$=$\frac{1}{2}$×($\frac{3}{4}$)2-1;
∵P2O2=O2O1=$\frac{1}{2}$P2O1=$\frac{1}{2}$×$\frac{3}{8}$=$\frac{3}{16}$,
∴AO2=AO1-O2O1=$\frac{3}{4}$-$\frac{3}{16}$=$\frac{9}{16}$,
∴AP3=P3O2=$\frac{1}{2}$AO2=$\frac{1}{2}$×$\frac{9}{16}$=$\frac{1}{2}$×($\frac{3}{4}$)3-1;
…
由此可得,APn=$\frac{1}{2}$×($\frac{3}{4}$)n-1,
故答案为:$\frac{1}{2}$×($\frac{3}{4}$)n-1.
点评 本题考查了图形的翻折变换,正方形的性质以及勾股定理的运用,解题过程中应注意折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

 名校课堂系列答案
名校课堂系列答案 如图,将正方形ABCD逆时针旋转得到正方形AB′C′D′,则旋转角度为( )
如图,将正方形ABCD逆时针旋转得到正方形AB′C′D′,则旋转角度为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
 如图,点B、E、C、F在同一直线上,BE=CF,∠B=∠F,再添加一个条件仍不能证明△ABC≌△DFE的是( )
如图,点B、E、C、F在同一直线上,BE=CF,∠B=∠F,再添加一个条件仍不能证明△ABC≌△DFE的是( )| A. | AB=DF | B. | ∠A=∠D | C. | AC∥DE | D. | AC=DE |
| A. | 射击运动员射击一次,命中9环 | |
| B. | 掷一枚普通的正方体骰子,向上的一面出现的点数大于6 | |
| C. | 在同一年出生的13名学生中,至少有2人出生在同一个月 | |
| D. | 买一张电影票,座位号是偶数号 |
| A. | 2分米 | B. | 2厘米 | C. | 2米 | D. | 2000米 |
| A. | k>1 | B. | k<1 | C. | k=1 | D. | k<1且k≠0 |