题目内容
在平原上,一门迫击炮发射的一发炮弹飞行的高度ym与飞行时间xs的关系满足y=-
x2+1Ox.
(1)经过多长时间,炮弹达到它的最高点?最高点的高度是多少?
(2)经过多长时间,炮弹落在地上爆炸?
| 1 |
| 5 |
(1)经过多长时间,炮弹达到它的最高点?最高点的高度是多少?
(2)经过多长时间,炮弹落在地上爆炸?
考点:二次函数的应用
专题:
分析:(1)将解析式y=-
x2+1Ox化为顶点式就可以求出最高点的高度和时间;
(2)当y=0时代入解析式就可以求出落在地上爆炸的时间.
| 1 |
| 5 |
(2)当y=0时代入解析式就可以求出落在地上爆炸的时间.
解答:解:(1)∵y=-
x2+1Ox.
∴y=-
(x2-50x),
∴y=-
(x-25)2+125.
∵a=-
<0,抛物线有最大值,
∴x=25时,y最大=125.
∴经过25s,炮弹达到它的最高点,最高点的高度是125米;
(2)当y=0时,-
x2+1Ox=0,
∴x1=0,x2=50.
∵x>0,
∴x=50
答:经过50s,炮弹落在地上爆炸.
| 1 |
| 5 |
∴y=-
| 1 |
| 5 |
∴y=-
| 1 |
| 5 |
∵a=-
| 1 |
| 5 |
∴x=25时,y最大=125.
∴经过25s,炮弹达到它的最高点,最高点的高度是125米;
(2)当y=0时,-
| 1 |
| 5 |
∴x1=0,x2=50.
∵x>0,
∴x=50
答:经过50s,炮弹落在地上爆炸.
点评:本题考查了二次函数的解析式的运用,二次函数的顶点式的运用,由函数值求自变量的值的运用,解答时将二次函数的一般式变为顶点式是关键.

练习册系列答案
相关题目
下列说法中,正确的是( )
| A、正方形是轴对称图形且有四条对称轴 |
| B、正方形的对角线是正方形的对称轴 |
| C、矩形是轴对称图形且有四条对称轴 |
| D、菱形的对角线相等 |
下列合并同类项正确的是( )
| A、2x2+3x4=5x6 |
| B、5xy2-3xy2=2 |
| C、7m2n-7mn2 |
| D、4ab2-5ab2=-ab2 |
 如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的
如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的 如图所示,将长方形纸片ABCD沿直线EF折叠,点C、D分别落在点C′、D′上,已知∠EFC=66°,求∠AED′的度数.
如图所示,将长方形纸片ABCD沿直线EF折叠,点C、D分别落在点C′、D′上,已知∠EFC=66°,求∠AED′的度数.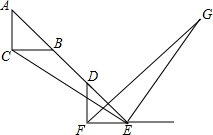 如图,△ABC是一个等腰直角三角形,∠ACB=90°,将△ABC沿AB方向平移到△DEF,连接CE.过点E作EG⊥CE交∠DFE的平分线于点G,试探究线段CE与EG的数量关系,并说明理由.
如图,△ABC是一个等腰直角三角形,∠ACB=90°,将△ABC沿AB方向平移到△DEF,连接CE.过点E作EG⊥CE交∠DFE的平分线于点G,试探究线段CE与EG的数量关系,并说明理由.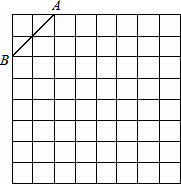 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作: