题目内容
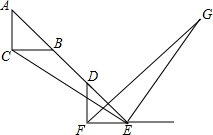 如图,△ABC是一个等腰直角三角形,∠ACB=90°,将△ABC沿AB方向平移到△DEF,连接CE.过点E作EG⊥CE交∠DFE的平分线于点G,试探究线段CE与EG的数量关系,并说明理由.
如图,△ABC是一个等腰直角三角形,∠ACB=90°,将△ABC沿AB方向平移到△DEF,连接CE.过点E作EG⊥CE交∠DFE的平分线于点G,试探究线段CE与EG的数量关系,并说明理由.考点:全等三角形的判定与性质
专题:常规题型
分析:根据等腰直角三角形的性质得AC=BC,∠A=45°,再根据平移的性质得BC=EF,BC∥EF,∠DFE=∠ACB=90°,则AC=EF,∠BCE=∠FEC,由EG⊥CE得到∠CEG=90°,所以∠ACE=∠FEG,由FG平分∠DFE得∠GFE=45°,则∠A=∠EFG,于是可根据“ASA”判断△ACE≌△FEG,所以CE=EG.
解答:解:CE=EG.理由如下:
∵△ABC是一个等腰直角三角形,
∴AC=BC,∠A=45°,
∵△ABC沿AB方向平移到△DEF,
∴BC=EF,BC∥EF,∠DFE=∠ACB=90°,
∴AC=EF,∠BCE=∠FEC,
∵EG⊥CE,
∴∠CEG=90°,
∴∠ACE=∠FEG,
而FG平分∠DFE,
∴∠GFE=45°,
∴∠A=∠EFG,
在△ACE和△FEG中,
,
∴△ACE≌△FEG(ASA),
∴CE=EG.
∵△ABC是一个等腰直角三角形,
∴AC=BC,∠A=45°,
∵△ABC沿AB方向平移到△DEF,
∴BC=EF,BC∥EF,∠DFE=∠ACB=90°,
∴AC=EF,∠BCE=∠FEC,

∵EG⊥CE,
∴∠CEG=90°,
∴∠ACE=∠FEG,
而FG平分∠DFE,
∴∠GFE=45°,
∴∠A=∠EFG,
在△ACE和△FEG中,
|
∴△ACE≌△FEG(ASA),
∴CE=EG.
点评:本题考查了全等三角形的判定与性质:判断三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”.也考查了等腰直角三角形的性质和平移的性质.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
下列说法不正确的是( )
| A、平行四边形对边平行 |
| B、两组对边平行的四边形是平行四边形 |
| C、平行四边形对角相等 |
| D、一组对角相等的四边形是平行四边形 |
 抛物线y=-(x-1)2+4与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为点D.
抛物线y=-(x-1)2+4与x轴相交于A、B两点(点A在点B的左侧),与y轴相交于点C,顶点为点D.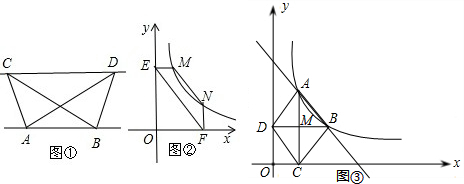
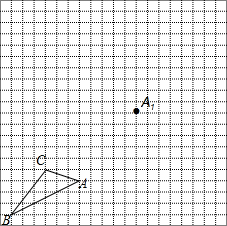 如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.
如图,在由边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)和点A1.