题目内容
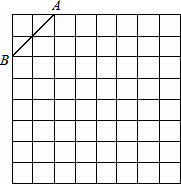 如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:
如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作:(1)在网格中建立平面直角坐标系,使A点坐标为(-2,4),B点坐标为(-4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则C点坐标是
(3)△ABC的周长=
(4)画出△ABC关于关于y轴对称的△A′B′C′.
考点:作图-轴对称变换
专题:
分析:(1)把点A向右平移2个单位,向下平移4个单位就是原点的位置,建立相应的平面直角坐标系;
(2)作线段AB的垂直平分线,寻找满足腰长是无理数的点C即可;
(3)利用格点三角形分别求出三边的长度,即可求出△ABC的周长;
(4)分别找出A、B、C关于y轴的对称点,顺次连接即可.
(2)作线段AB的垂直平分线,寻找满足腰长是无理数的点C即可;
(3)利用格点三角形分别求出三边的长度,即可求出△ABC的周长;
(4)分别找出A、B、C关于y轴的对称点,顺次连接即可.
解答:解:(1)如图所示,建立平面直角坐标系;

(2)点C的坐标为(-1,1);
(3)AB=
=2
,
BC=AC=
=
,
则△ABC的周长=2
+2
;
(4)△A'B'C'如图所示.

(2)点C的坐标为(-1,1);
(3)AB=
| 22+22 |
| 2 |
BC=AC=
| 12+32 |
| 10 |
则△ABC的周长=2
| 2 |
| 10 |
(4)△A'B'C'如图所示.
点评:本题考查的是作图-轴对称变换,熟知轴对称变换的性质是解答此题的关键.

练习册系列答案
相关题目




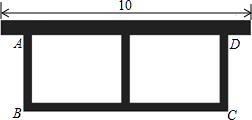 如图,园艺工人利用长24m的篱笆,一面利用墙(墙的最大长度为10m),围成中间隔有一道篱笆的长方形花圃,用以种植红玫瑰和蓝玫瑰.设花圃的边AB长为xm,BC边长为ym.
如图,园艺工人利用长24m的篱笆,一面利用墙(墙的最大长度为10m),围成中间隔有一道篱笆的长方形花圃,用以种植红玫瑰和蓝玫瑰.设花圃的边AB长为xm,BC边长为ym.
 如图,抛物线
如图,抛物线 甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快
甲、乙两人分别从A、B两地相向而行,y与x的函数关系如图,其中x表示乙行走的时间(时),y表示两人与A地的距离(千米),甲的速度比乙每小时快