题目内容
7. 如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.
如图,在△ABC中,∠ACB=90°,CD⊥AB垂足为D,AE平分∠CAB交CD于点F,交BC于点E,EH⊥AB,垂足为H,连接FH.求证:(1)CF=CE
(2)四边形CFHE是平行四边形.
分析 (1)利用垂直的定义结合角平分线的性质以及互余的性质得出∠4=∠5,进而得出答案;
(2)根据题意分别得出CF∥EH,CF=EH,进而得出答案.
解答 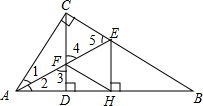 证明:(1)如图所示:∵∠ACB=90°,CD⊥AB垂足为D,
证明:(1)如图所示:∵∠ACB=90°,CD⊥AB垂足为D,
∴∠1+∠5=90°,∠2+∠3=90°,
又∵∠AE平分∠CAB,
∴∠1=∠2,
∴∠3=∠5,
∵∠3=∠4,
∴∠4=∠5,
∴CF=CE;
(2)∵AE平分∠CAB,CE⊥AC,EH⊥AB,
∴CE=EH,
由(1)CF=CE,
∴CF=EH,
∵CD⊥AB,EH⊥AB,
∴∠CDB=90°,∠EHB=90°,
∴∠CDB=∠EHB,
∴CD∥EH,
即CF∥EH,
∴四边形CFHE是平行四边形.
点评 本题考查了平行四边形的性质、角平分线性质等知识点的应用,熟练应用等腰三角形的性质是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.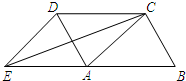 已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
 已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )
已知:如图,四边形ABCD是平行四边形,延长BA到点E,使AE=AB,联结ED、EC、AC.添加一个条件,能使四边形ACDE成为矩形的是( )| A. | AC=CD | B. | AB=AD | C. | AD=AE | D. | BC=CE. |
15.下列长度的三条线段能组成三角形的是( )
| A. | 1.5cm,2cm,2.5cm | B. | 2cm,5cm,8cm | C. | 1cm,3cm,4cm | D. | 5cm,3cm,1cm |
2.下列命题不正确的是( )
| A. | 两直线平行,同位角相等 | |
| B. | 两点之间直线最短 | |
| C. | 对顶角相等 | |
| D. | 从直线外一点到直线上的所有线段中,垂线段最短 |
19.下列命题是假命题的是( )
| A. | 三角形的三条角平分线相交于一点,并且这一点到三边距离相等 | |
| B. | 等腰三角形底边的中点到两腰的距离相等 | |
| C. | 面积相等的两个三角形全等 | |
| D. | 一个三角形中至少有两个锐角 |
 如图,在菱形ABCD中,AC=8,BD=6,DP⊥AB于点P,求PB.
如图,在菱形ABCD中,AC=8,BD=6,DP⊥AB于点P,求PB. 已知:如图,在?ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.
已知:如图,在?ABCD中,AE⊥BC,CF⊥AD,垂足分别为E、F,AE、CF分别与BD相交于点G、H,联结AH、CG.