题目内容
15.观察下列等式:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$;将以上三个等式两边分别相加得:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$;
(1)猜想并写出:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$.
(2)直接写出下列各式的计算结果:
①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2014×2015}$=$\frac{2014}{2015}$;
②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$=$\frac{n}{n+1}$.
(3)探究并计算式子:$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{2013×2015}$的值.
分析 (1)观察已知等式,得到一般性规律,写出即可;
(2)两式利用得出的规律变形,计算即可得到结果;
(3)原式变形后,利用得出的规律化简,计算即可得到结果.
解答 解:(1)猜想得:$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$;
(2)①原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$=1-$\frac{1}{2015}$=$\frac{2014}{2015}$;
②原式=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$;
(3)原式=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2013}$-$\frac{1}{2015}$)=$\frac{1}{2}$(1-$\frac{1}{2015}$)=$\frac{1007}{2015}$.
故答案为:(1)$\frac{1}{n}$-$\frac{1}{n+1}$;(2)①$\frac{2014}{2015}$;②$\frac{n}{n+1}$.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
3.下列四个多项式,能因式分解的是( )
| A. | a2+b2 | B. | a2-a+2 | C. | a2+3b | D. | (x+y)2-4 |
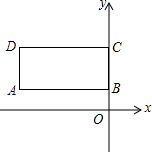 如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1,点A关于x轴的对称点A′坐标是((-4,-1));点D坐标是((-4,3)),点D到原点的距离是5.
如图,矩形ABCD中,点A(-4,1)、B(0,1)、C(0,3),则点A到x轴的距离是1,点A关于x轴的对称点A′坐标是((-4,-1));点D坐标是((-4,3)),点D到原点的距离是5. 画一个正方形,使它的面积是图中正方形面积的4倍.
画一个正方形,使它的面积是图中正方形面积的4倍.