题目内容
9. 如图,为了测量黄河某一段河流宽度,在河北选了一点A,在河南岸相距200m的B、C两点,分别测得∠ABC=60°,∠ACB=45°,求这段河流的宽度.
如图,为了测量黄河某一段河流宽度,在河北选了一点A,在河南岸相距200m的B、C两点,分别测得∠ABC=60°,∠ACB=45°,求这段河流的宽度.
分析 过A作AD⊥BC于D,根据∠ABC=60°,∠ACB=45°求出BD、CD与AD关系,根据BC=200m,可以求得AD的长度,即可解题.
解答 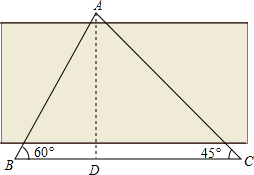 解:过A作AD⊥BC于D,
解:过A作AD⊥BC于D,
∵在Rt△ADB中,∠B=60°,
∴∠BAD=30°,
∴BD=AD•tan30°=$\frac{\sqrt{3}}{3}$AD,
∵在Rt△ADC中,∠C=45°,
∴CD=AD,
又BC=200,
∴BD+CD=$\frac{\sqrt{3}}{3}$AD+AD=200,
解得AD=300-100$\sqrt{3}$.
答:这段河流的宽度为(300-100$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用,解本题关键是构建直角三角形,利用三角函数来解答.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
17.将2x2-x-2分解因式为( )
| A. | $({x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}})({x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}})$ | B. | $2({x+\frac{1}{4}-\frac{{\sqrt{17}}}{4}})({x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}})$ | ||
| C. | $2({x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}})({x+\frac{1}{4}-\frac{{\sqrt{17}}}{4}})$ | D. | $2({x-\frac{1}{4}+\frac{{\sqrt{17}}}{4}})({x-\frac{1}{4}-\frac{{\sqrt{17}}}{4}})$ |
1.已知抛物线y=-2x2+12x-13,则下列关于此抛物线说法正确的是( )
| A. | 开口向下,对称轴为直线x=-3 | B. | 顶点坐标为(-3,5) | ||
| C. | 最小值为5 | D. | 当x>3时,y随x的增大而减小 |
 如图所示,?ABCD中,∠ADC和∠BCD的平分线交于点M,且分别交AB于E、F.
如图所示,?ABCD中,∠ADC和∠BCD的平分线交于点M,且分别交AB于E、F.
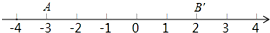 操作与探究:对数轴上的点P进行如下操作:先把点P表示的数乘以2,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.
操作与探究:对数轴上的点P进行如下操作:先把点P表示的数乘以2,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.