题目内容
19.如图①,将边长为2的正方形OABC如图①放置,O为原点.(Ⅰ)若将正方形OABC绕点O逆时针旋转60°时,如图②,求点A的坐标;
(Ⅱ)如图③,若将图①中的正方形OABC绕点O逆时针旋转75°时,求点B的坐标.

分析 (1)过点A作x轴的垂线,垂足为D,∠ADO=90°,根据旋转角得出∠AOD=30°,进而得到AD=$\frac{1}{2}$AO=1,DO=$\sqrt{3}$,据此可得点A的坐标;
(2)连接BO,过B作BD⊥y轴于D,根据旋转角为75°,可得∠BOD=30°,根据勾股定理可得BO=2$\sqrt{2}$,再根据Rt△BOD中,BD=$\sqrt{2}$,OD=$\sqrt{6}$,可得点B的坐标.
解答  解:(1)过点A作x轴的垂线,垂足为D,∠ADO=90°,
解:(1)过点A作x轴的垂线,垂足为D,∠ADO=90°,
∵旋转角为60°,
∴∠AOD=90°-60°=30°,
∴AD=$\frac{1}{2}$AO=1,DO=$\sqrt{3}$,
∴A(-$\sqrt{3}$,1);
(2)连接BO,过B作BD⊥y轴于D,
∵旋转角为75°,∠AOB=45°,
∴∠BOD=75°-45°=30°,
∵∠A=90°,AB=AO=2,
∴BO=2$\sqrt{2}$,
∴Rt△BOD中,BD=$\sqrt{2}$,OD=$\sqrt{6}$,
∴B(-$\sqrt{2}$,$\sqrt{6}$).
点评 本题主要考查了旋转变换以及正方形的性质,解决问题的关键是作辅助线构造直角三角形,解题时注意:正方形的四条边都相等,四个角都是直角.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 如图,一次函数的图象经过(2,0)和(0,-4),根据图象求$\sqrt{{k}^{2}-2kb+{b}^{2}}$的值.
如图,一次函数的图象经过(2,0)和(0,-4),根据图象求$\sqrt{{k}^{2}-2kb+{b}^{2}}$的值. 如图,一次函数与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点. 某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.
某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满200元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转盘,那么可直接获得10元的购物券.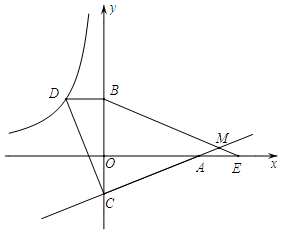 如图,已知点D在反比例函数y=$\frac{m}{x}$的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=$\frac{2}{5}$.
如图,已知点D在反比例函数y=$\frac{m}{x}$的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=$\frac{2}{5}$.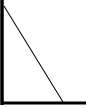 如图,一长梯靠在墙上,当梯子底端距离墙脚5米时,梯子的顶端高出地面9米;现梯子的顶端向上移动1米,求此时梯子的底端与墙脚的距离.
如图,一长梯靠在墙上,当梯子底端距离墙脚5米时,梯子的顶端高出地面9米;现梯子的顶端向上移动1米,求此时梯子的底端与墙脚的距离. 如图,已知:∠C=∠D,∠D=∠1,说明:AC∥DF,DB∥EC.
如图,已知:∠C=∠D,∠D=∠1,说明:AC∥DF,DB∥EC.