题目内容
8.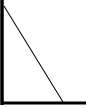 如图,一长梯靠在墙上,当梯子底端距离墙脚5米时,梯子的顶端高出地面9米;现梯子的顶端向上移动1米,求此时梯子的底端与墙脚的距离.
如图,一长梯靠在墙上,当梯子底端距离墙脚5米时,梯子的顶端高出地面9米;现梯子的顶端向上移动1米,求此时梯子的底端与墙脚的距离.
分析 设此时梯子的底端与墙脚的距离为xm,再由勾股定理求出x的值即可.
解答 解:设此时梯子的底端与墙脚的距离为xm,
∵梯子底端距离墙脚5米时,梯子的顶端高出地面9米,
∴52+92=(9+1)2+x2,解得x=$\sqrt{6}$(m).
答:此时梯子的底端与墙脚的距离为$\sqrt{6}$m.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,领会数形结合的思想的应用.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
18.计算(-$\frac{5}{13}$)100×(-$\frac{13}{5}$)101所得结果为( )
| A. | 1 | B. | -1 | C. | -2$\frac{3}{5}$ | D. | -$\frac{5}{13}$ |
14.已知△ABC中,AB=5,AC=7,BC=a,则a的取值范围是( )
| A. | 1<a<6 | B. | 5<a<7 | C. | 2<a<12 | D. | 10<a<14 |

 如图.在正方形ABCD中,点P是BC延长线上一点,BQ⊥PD于点Q,QN⊥BD于点N,连接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,则AN的长为$\sqrt{10}$.
如图.在正方形ABCD中,点P是BC延长线上一点,BQ⊥PD于点Q,QN⊥BD于点N,连接AN.若S△DMQ=$\frac{1}{8}$DM2,AB=4,则AN的长为$\sqrt{10}$.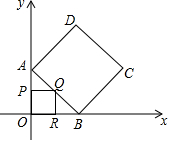 如图,在直角坐标系中,已知A(0,4)、B(4,0),以AB为边在第一象限内作正方形ABCD,在三角形AOB内部做正方形OPQR,使P、R、Q三点分别在线段OA、OB、AB上,将正方形OPQR绕点O顺时针旋转时,求点C到点Q距离的最大值与最小值.
如图,在直角坐标系中,已知A(0,4)、B(4,0),以AB为边在第一象限内作正方形ABCD,在三角形AOB内部做正方形OPQR,使P、R、Q三点分别在线段OA、OB、AB上,将正方形OPQR绕点O顺时针旋转时,求点C到点Q距离的最大值与最小值.