题目内容
10. 如图,一次函数的图象经过(2,0)和(0,-4),根据图象求$\sqrt{{k}^{2}-2kb+{b}^{2}}$的值.
如图,一次函数的图象经过(2,0)和(0,-4),根据图象求$\sqrt{{k}^{2}-2kb+{b}^{2}}$的值.
分析 先根据题意得出一次函数的解析式,求出k、b的值,再代入代数式进行计算即可.
解答 解:∵一次函数的图象经过(2,0)和(0,-4),
∴$\left\{\begin{array}{l}{2k+b=0}\\{b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=-4}\end{array}\right.$.
∵k2-2kb+b2=(k-b)2=(2+4)2=36,
∴$\sqrt{{k}^{2}-2kb+{b}^{2}}$=$\sqrt{36}$=6.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
20.已知三角形的两边分别为5和8,则此三角形的第三边可能是( )
| A. | 2 | B. | 3 | C. | 5 | D. | 13 |
18.计算(-$\frac{5}{13}$)100×(-$\frac{13}{5}$)101所得结果为( )
| A. | 1 | B. | -1 | C. | -2$\frac{3}{5}$ | D. | -$\frac{5}{13}$ |
2.近年来,我国持续大面积的雾霾天气让环境和健康问题称为社会关注的焦点,为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A非常了解B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
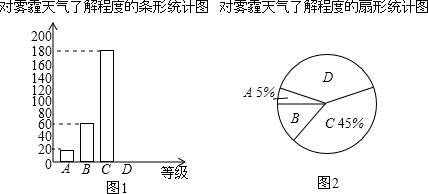
对雾霾所了解程度的统计表:
请结合统计图表,回答下列问题:
(1)求出本次参与调查的学生人数;
(2)请补全条形统计图;
(3)若该校共有2700名学生,根据抽样调查的结果,估计全校调查结果的等级为D的学生共有多少名?

对雾霾所了解程度的统计表:
| 对雾霾的了解程度 | 百分比 |
| A.非常了解 | 5% |
| A.比较了解 | 15% |
| C.基本了解 | 45% |
| D.不了解 | n |
(1)求出本次参与调查的学生人数;
(2)请补全条形统计图;
(3)若该校共有2700名学生,根据抽样调查的结果,估计全校调查结果的等级为D的学生共有多少名?
 如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
如图,△ABC的三个顶点的坐标分别是A(-2,-4),B(0,-4),C(1,-1).
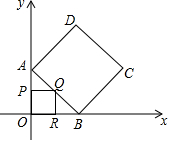 如图,在直角坐标系中,已知A(0,4)、B(4,0),以AB为边在第一象限内作正方形ABCD,在三角形AOB内部做正方形OPQR,使P、R、Q三点分别在线段OA、OB、AB上,将正方形OPQR绕点O顺时针旋转时,求点C到点Q距离的最大值与最小值.
如图,在直角坐标系中,已知A(0,4)、B(4,0),以AB为边在第一象限内作正方形ABCD,在三角形AOB内部做正方形OPQR,使P、R、Q三点分别在线段OA、OB、AB上,将正方形OPQR绕点O顺时针旋转时,求点C到点Q距离的最大值与最小值.