题目内容
按要求解答下列问题：
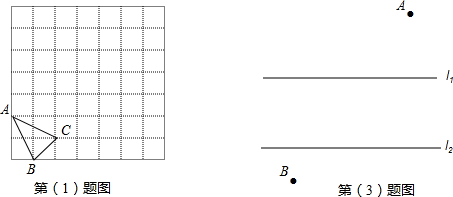
（1）分别按下列要求作出经过平移后的图形
①把三角形ABC向右平移3格．
②把第①题所得图形向上平移4格．
（2）经（1）中二次平移后所得的图形，能通过三角形ABC一次平移得到吗？如果你认为可以，描述这个平移过程．
（3）如图：直线l1，l2表示一条河的两岸，且l1∥l2，现要在河上建一座桥．桥建在何处才能使从村庄A经过河到村庄B的路程最短？画出示意图，并用平移的原理说明理由．
（1）分别按下列要求作出经过平移后的图形
①把三角形ABC向右平移3格．
②把第①题所得图形向上平移4格．
（2）经（1）中二次平移后所得的图形，能通过三角形ABC一次平移得到吗？如果你认为可以，描述这个平移过程．
（3）如图：直线l1，l2表示一条河的两岸，且l1∥l2，现要在河上建一座桥．桥建在何处才能使从村庄A经过河到村庄B的路程最短？画出示意图，并用平移的原理说明理由．
考点：作图—应用与设计作图,利用平移设计图案
专题：
分析：（1）根据图形平移的性质画出平移后的图形即可；
（2）根据平移前后的图形特点即可得出结论．
（3）先确定AA′=CD，且AA′∥CD，连接BA′，与河岸的交点就是点C，过点C作CD垂直河岸，交另一河岸于点D，CD就是所求的桥的位置．
（2）根据平移前后的图形特点即可得出结论．
（3）先确定AA′=CD，且AA′∥CD，连接BA′，与河岸的交点就是点C，过点C作CD垂直河岸，交另一河岸于点D，CD就是所求的桥的位置．
解答：解：（1）如图，
（2）由图可知，将△ABC沿直线AA″的方向平移线段AA″的长即可．
（3）先确定AA′=CD，且AA′∥CD，连接BA′，与河岸的交点就是点C，过点C作CD垂直河岸，交另一河岸于点D，CD就是所求的桥的位置．如图（3）
根据“两点之间线段最短”，A′B最短，即AD+BC最短．
（2）由图可知，将△ABC沿直线AA″的方向平移线段AA″的长即可．
（3）先确定AA′=CD，且AA′∥CD，连接BA′，与河岸的交点就是点C，过点C作CD垂直河岸，交另一河岸于点D，CD就是所求的桥的位置．如图（3）
根据“两点之间线段最短”，A′B最短，即AD+BC最短．
点评：本题考查的是作图-平移变换，熟知图形平移不变性的性质是解答此题的关键．
练习册系列答案
相关题目
抛物线y=（x-3）2+5的开口方向，对称轴，顶点坐标分别是（ ）
| A、开口向上；x=-3；（-3，5） |
| B、开口向上；x=3；（3，5） |
| C、开口向下；x=3；（-3，-5） |
| D、开口向下；x=-3；（3，-5） |
下列运算正确的是（ ）
A、
| ||
| B、（a+b）2=a2+b2 | ||
| C、x6÷x3=x2 | ||
D、
|
如图，在△ABC中，分别以AB、AC、BC为边在BC的同侧作等边△ABE、等边△ACD、等边△BCF．