题目内容
如图,将一块腰长为
的等腰直角三角板ABC放在平面直角坐标系中,点A在y轴正半轴上,直角顶点C的坐标为(-2,0),点B在第二象限.
(1)求点A,点B的坐标.
(2)将△ABC沿x轴正方向平移后得到△A′B′C′,点A′,B′恰好落在反比例函数y=
的图象上,求平移的距离和反比例函数的解析式.

| 5 |
(1)求点A,点B的坐标.
(2)将△ABC沿x轴正方向平移后得到△A′B′C′,点A′,B′恰好落在反比例函数y=
| k |
| x |

考点:反比例函数综合题
专题:综合题
分析:(1)过B点作BH⊥x轴于H,在Rt△AOC中,根据勾股定理得到OA=1,则A点坐标为(0,1);在根据等腰直角三角形的性质得CB=CA,∠ACB=90°,则可利用等角的余角相等得∠ACO=∠HBC,于是可根据“AAS”判断△BCH≌△CAO,所以CH=OA=1,BH=OC=2,OH=HC+OC=3,由此得到B点为(-3,2);
(2)设将△ABC沿x轴正方向平移a个单位后得到△A′B′C′,根据平移的性质得B′的坐标为(-3+a,2),C′点的坐标为(a,1),由于点A′,B′恰好落在反比例函数y=
的图象上,则根据反比例函数图象上点的坐标特征得到k=2×(-3+a)=1×a,解得a=6,所以k=6,于是得到反比例函数的解析式为y=
.
(2)设将△ABC沿x轴正方向平移a个单位后得到△A′B′C′,根据平移的性质得B′的坐标为(-3+a,2),C′点的坐标为(a,1),由于点A′,B′恰好落在反比例函数y=
| k |
| x |
| 6 |
| x |
解答: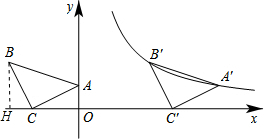 解:(1)过B点作BH⊥x轴于H,如图,
解:(1)过B点作BH⊥x轴于H,如图,
∵C的坐标为(-2,0),
∴OC=2,
在Rt△AOC中,AC=
,
∴OA=
=1,
∴A点坐标为(0,1);
∵△ACB为等腰直角三角形,
∴CB=CA,∠ACB=90°,
∴∠BCH+∠ACO=90°,
而∠BCH+∠HBC=90°,
∴∠ACO=∠HBC,
在△BCH和△CAO中,
,
∴△BCH≌△CAO(AAS),
∴CH=OA=1,BH=OC=2,
∴OH=HC+OC=3,
∴B点为(-3,2);
(2)设将△ABC沿x轴正方向平移a个单位后得到△A′B′C′,则B′的坐标为(-3+a,2),C′点的坐标为(a,1),
∵点A′,B′恰好落在反比例函数y=
的图象上,
∴2×(-3+a)=1×a,解得a=6,
∴k=1×6=6,
∴反比例函数的解析式为y=
.
 解:(1)过B点作BH⊥x轴于H,如图,
解:(1)过B点作BH⊥x轴于H,如图,∵C的坐标为(-2,0),
∴OC=2,
在Rt△AOC中,AC=
| 5 |
∴OA=
| AC2-OC2 |
∴A点坐标为(0,1);
∵△ACB为等腰直角三角形,
∴CB=CA,∠ACB=90°,
∴∠BCH+∠ACO=90°,
而∠BCH+∠HBC=90°,
∴∠ACO=∠HBC,
在△BCH和△CAO中,
|
∴△BCH≌△CAO(AAS),
∴CH=OA=1,BH=OC=2,
∴OH=HC+OC=3,
∴B点为(-3,2);
(2)设将△ABC沿x轴正方向平移a个单位后得到△A′B′C′,则B′的坐标为(-3+a,2),C′点的坐标为(a,1),
∵点A′,B′恰好落在反比例函数y=
| k |
| x |
∴2×(-3+a)=1×a,解得a=6,
∴k=1×6=6,
∴反比例函数的解析式为y=
| 6 |
| x |
点评:本题考查了反比例函数的综合题:熟练掌握反比例函数图象上点的坐标特征、等腰直角三角形的性质和平移的性质;会运用全等三角形的判定与性质解决线段相等的问题,利用勾股定理计算线段的长.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
己知点(-4,y1),(2,y2),(3,y3)在反比例函数y=
的图象上.下列结论正确的是( )
| -k2-4 |
| x |
| A、y1<y2<y3 |
| B、y1<y3<y2 |
| C、y1>y2>y3 |
| D、y1>y3>y2 |
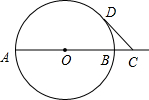 已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA. 为增强市民的节能意识,我市试行阶梯电价.从2013年开始,按照每户每年的用电量分三个档次计费,具体规定见右图.小明统计了自己2013年前5个月的实际用电量为1300度,请帮助小明分析下面问题.
为增强市民的节能意识,我市试行阶梯电价.从2013年开始,按照每户每年的用电量分三个档次计费,具体规定见右图.小明统计了自己2013年前5个月的实际用电量为1300度,请帮助小明分析下面问题. 如图,△ABC,△EBF是两个等边三角形,D是BC上一点,且DC=BF,求证:△AED是等边三角形.
如图,△ABC,△EBF是两个等边三角形,D是BC上一点,且DC=BF,求证:△AED是等边三角形.