题目内容
在△ABC中,AB=AC,∠BAC=α(0°<α<60°),点D为△ABC内一点,BD=BC,且∠CBD=60°.
(1)如图1,求∠ABD的大小(用含α的式子表示);
(2)求证:AD是BC的垂直平分线;
(3)如图2,以AB为一边作等边三角形ABE,连接CE,DE,试探究AD、BD、DE之间有怎样的数量关系?
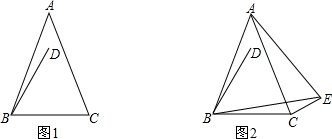
(1)如图1,求∠ABD的大小(用含α的式子表示);
(2)求证:AD是BC的垂直平分线;
(3)如图2,以AB为一边作等边三角形ABE,连接CE,DE,试探究AD、BD、DE之间有怎样的数量关系?
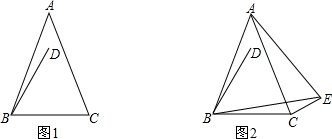
考点:全等三角形的判定与性质,等腰三角形的性质,等边三角形的判定与性质,勾股定理
专题:
分析:(1)求出∠ABC的度数,即可求出答案;
(2)由BD=BC,且∠CBD=60°求得△BCD为等边三角形,然后求得△ABD≌△ACD,从而求得∠BAD=∠CAD,根据等腰三角形三线合一,即可求得.
(3))由△ABE是等边三角形,△BCD为等边三角形,可求得∠ABD=∠EBC,然后通过三角形全等,求得∠BAD=∠BEC,AD=CE,根据∠ABD=∠EBC=30°-
α,∠BAD=∠BEC=
α,求得∠BCE=150°,由于△BCD为等边三角形,从而△BCD是直角三角形,即可求得AD、BD、DE之间的数量关系.
(2)由BD=BC,且∠CBD=60°求得△BCD为等边三角形,然后求得△ABD≌△ACD,从而求得∠BAD=∠CAD,根据等腰三角形三线合一,即可求得.
(3))由△ABE是等边三角形,△BCD为等边三角形,可求得∠ABD=∠EBC,然后通过三角形全等,求得∠BAD=∠BEC,AD=CE,根据∠ABD=∠EBC=30°-
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)∵AB=AC,∠A=α,
∴∠ABC=∠ACB=
(180°-∠A)=90°-
α,
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,
即∠ABD=30°-
α;
(2)证明:如图1,连接AD,CD,
∵BD=BC,且∠CBD=60°.
∴△BCD为等边三角形,
在△ABD与△ACD中
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∵AB=AC,
∴AD是BC的垂直平分线;

(3)如图2,连接AD、DC、DE,
∵△ABE是等边三角形,△BCD为等边三角形,
∴∠ABE=∠DBC=60°,
∴∠ABD=∠EBC,
在△ABD与△EBC中
∴△ABD≌△EBC(SAS)
∴∠BAD=∠BEC,AD=CE,
∴∠ABD=∠EBC=30°-
α,∠BAD=∠BEC=
α,
∴∠BCE=180°-∠EBC-∠BEC=180°-(30°-
α)-
α=150°,
∴∠DCE=150°-60°=90°,
∴△DCE是直角三角形,
∴CD2+CE2=DE2,
∵BD=CD,AD=CE,
∴DB2+AD2=DE2.

解:(1)∵AB=AC,∠A=α,
∴∠ABC=∠ACB=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠ABD=∠ABC-∠DBC,∠DBC=60°,
即∠ABD=30°-
| 1 |
| 2 |
(2)证明:如图1,连接AD,CD,
∵BD=BC,且∠CBD=60°.
∴△BCD为等边三角形,
在△ABD与△ACD中
|
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,
∵AB=AC,
∴AD是BC的垂直平分线;

(3)如图2,连接AD、DC、DE,
∵△ABE是等边三角形,△BCD为等边三角形,
∴∠ABE=∠DBC=60°,
∴∠ABD=∠EBC,
在△ABD与△EBC中
|
∴△ABD≌△EBC(SAS)
∴∠BAD=∠BEC,AD=CE,
∴∠ABD=∠EBC=30°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BCE=180°-∠EBC-∠BEC=180°-(30°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠DCE=150°-60°=90°,
∴△DCE是直角三角形,
∴CD2+CE2=DE2,
∵BD=CD,AD=CE,
∴DB2+AD2=DE2.
点评:此题考查了全等三角形的判定与性质,等边三角形的性质和判定,等腰直角三角形的判定和性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=
| 1 |
| 4 |
其中正确结论的是( )
| A、①②③ | B、①②④ |
| C、①③④ | D、②③④ |
下列运算中,结果正确的是( )
| A、x+x2=x3 |
| B、4x-x=3x |
| C、x2•x3=x6 |
| D、x4÷x3=x2 |
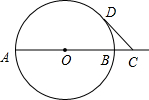 已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.
已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA. 如图,△ABC,△EBF是两个等边三角形,D是BC上一点,且DC=BF,求证:△AED是等边三角形.
如图,△ABC,△EBF是两个等边三角形,D是BC上一点,且DC=BF,求证:△AED是等边三角形.
 如图,反比例函数y=
如图,反比例函数y=