题目内容
18. 如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°
如图,BD丄AC 于D,EF丄AC 于F.∠AMD=∠AGF.∠1=∠2=35°(1)求∠GFC的度数:
(2)求证:DM∥BC.
分析 (1)由BD⊥AC,EF⊥AC,得到BD∥EF,根据平行线的性质得到∠EFG=∠1=35°,再根据角的和差关系可求∠GFC的度数;
(2)根据平行线的性质得到∠2=∠CBD,等量代换得到∠1=∠CBD,根据平行线的判定定理得到GF∥BC,证得MD∥GF,根据平行线的性质即可得到结论.
解答 解:(1)∵BD⊥AC,EF⊥AC,
∴BD∥EF,
∴∠EFG=∠1=35°,
∴∠GFC=90°+35°=125°;
(2)∵BD∥EF,
∴∠2=∠CBD,
∴∠1=∠CBD,
∴GF∥BC,
∵∠AMD=∠AGF,
∴MD∥GF,
∴DM∥BC.
点评 本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
 在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )
在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上.已知正方形A1B1C1D1的边长为1,∠C1B1O=30°,B1C1∥B2C2∥B3C3…则正方形A2016B2016C2016D2016的边长是( )| A. | ${(\frac{1}{2})}^{2015}$ | B. | ${(\frac{1}{2})}^{2016}$ | C. | ${(\frac{\sqrt{3}}{3})}^{2015}$ | D. | ${(\frac{\sqrt{3}}{3})}^{2016}$ |
3.已知下列三角形的各边长:
①3、4、5,②5、12、13,③3、4、6,④5、11、12
其中直角三角形有( )
①3、4、5,②5、12、13,③3、4、6,④5、11、12
其中直角三角形有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
8. 如图,点A(1,m),B(2,n)在一次函数y=kx+b的图象上,则( )
如图,点A(1,m),B(2,n)在一次函数y=kx+b的图象上,则( )
 如图,点A(1,m),B(2,n)在一次函数y=kx+b的图象上,则( )
如图,点A(1,m),B(2,n)在一次函数y=kx+b的图象上,则( )| A. | m=n | B. | m>n | ||
| C. | m<n | D. | m、n的大小关系不确定 |
 已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.
已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.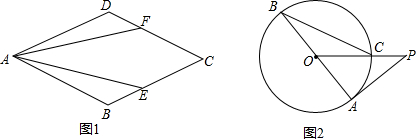
 如图,在矩形ABCD中,AD=2AB,E是AD上一点,且BE=BC,则∠ECD的度数是15°.
如图,在矩形ABCD中,AD=2AB,E是AD上一点,且BE=BC,则∠ECD的度数是15°.