题目内容
15.已知一个三次多项式除以x2-9的余式为3x-5,除以x2-16余式-2x-7,求这个三次多项式.分析 设所求三次多项式A=ax3+bx2+cx+d(a≠0),A除以x2-9,x2-16时,商式分别为ax+m,ax+n,则ax3+bx2+cx+d=(x2-9)(ax+m)+3x-5①,ax3+bx2+cx+d=(x2-16)(ax+n)-2x-7②,用特值法列出方程组,从而确定a,b,c,d这4个系数.
解答 解:设所求三次多项式A=ax3+bx2+cx+d(a≠0),
A除以x2-9,x2-16时,商式分别为ax+m,ax+n,
则ax3+bx2+cx+d=(x2-9)(ax+m)+3x-5①,
ax3+bx2+cx+d=(x2-16)(ax+n)-2x-7②,
在①式中分别取x=3,-3时,
27a+9b+3c+d=4③,
-27a+9b-3c+d=-1④,
在②式中分别取x=4,-4时,
64a+16b+4c+d=-15⑤,
-64a+16b-4c+d=1⑥,
联立③④⑤⑥,解得:a=-$\frac{17}{42}$,b=-$\frac{17}{14}$,c=$\frac{94}{21}$,d=$\frac{87}{7}$.
故所求的三次多项式为-$\frac{17}{42}$x3-$\frac{17}{14}$x2+$\frac{94}{21}$x+$\frac{87}{7}$.
点评 本题考查多项式的除法,弄清被除式、除式、商、余式四者之间的关系是解题的关键.其中(3)用特值法列方程组求解,难度较大.

练习册系列答案
相关题目
5.下列各组数中,不是互为相反意义的量的是( )
| A. | 向东走20千米与向西走15千米 | B. | 收入200元与亏损30元 | ||
| C. | 超过0.05mm与不足0.03mm | D. | 上升10米和下降7米 |
 如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是15.
如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是15.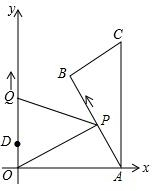 如图,Rt△ABC中,∠B=90°,∠CAB=30°,AC⊥x轴,它的顶点A的坐标为(10,0),C(10,$\frac{20\sqrt{3}}{3}$),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,若P点的速度为2单位/秒,设P运动的时间为t秒.
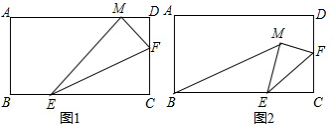
如图,Rt△ABC中,∠B=90°,∠CAB=30°,AC⊥x轴,它的顶点A的坐标为(10,0),C(10,$\frac{20\sqrt{3}}{3}$),点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,若P点的速度为2单位/秒,设P运动的时间为t秒. 尺规作图:如图,BC是四边形ABCD的最大边,试以BC为一边用尺规作一个三角形,使它的面积等于四边形ABCD的面积.
尺规作图:如图,BC是四边形ABCD的最大边,试以BC为一边用尺规作一个三角形,使它的面积等于四边形ABCD的面积. 如图,菱形ABCD的边长为5,对角线AC=8.
如图,菱形ABCD的边长为5,对角线AC=8.