题目内容
7. 如图,菱形ABCD的边长为5,对角线AC=8.
如图,菱形ABCD的边长为5,对角线AC=8.(1)用尺规作出经过A、B、C三点的圆;
(2)求这个圆的半径的长;
(3)判断点D和这个圆的位置关系,并说明理由.
分析 (1)直接利用三角形外接圆的作法得出圆心位置,进而得出答案;
(2)直接利用相似三角形的判定与性质结合菱形的性质得出半径长;
(3)利用点与圆的位置关系判定方法得出答案.
解答 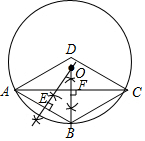 解:(1)如图所示:⊙O即为所求;
解:(1)如图所示:⊙O即为所求;
(2)由题意可得:∠ABF=∠OBE,∠DEB=∠AFB=90°,
故△OEB∽△AFB,
则$\frac{BE}{BF}$=$\frac{AB}{OB}$,
∵菱形ABCD的边长为5,对角线AC=8,
∴AF=4,则BF=3,BE=$\frac{5}{2}$,
∴$\frac{\frac{5}{2}}{3}$=$\frac{BO}{5}$,
解得:BO=$\frac{25}{6}$,
即这个圆的半径的长为$\frac{25}{6}$;
(3)点D在圆内,
理由:∵菱形ABCD的边长为5,对角线AC=8,
∴AF=4,则BF=3,
∴BD=6,
∴DO=6-$\frac{25}{6}$=$\frac{11}{6}$<$\frac{25}{6}$,
∴点D在圆内.
点评 此题主要考查了复杂作图以及菱形的性质以及相似三角形的判定与性质等知识,正确掌握相似三角形的判定与性质是解题关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
18. 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
 如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修一个货站P,使得货站P到两公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货运站P的位置.(保留作图痕迹)
2.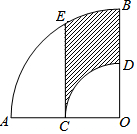 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )
 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为( )| A. | $\frac{4π-3\sqrt{3}}{4}$ | B. | $\frac{π-\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$+$\frac{π}{12}$ | D. | $\frac{π-3\sqrt{3}}{2}$ |
16.点(2,5),(4,5)是抛物线y=ax2+bx+c上的两点,那么该抛物线的对称轴为( )
| A. | x=-$\frac{b}{a}$ | B. | x=1 | C. | x=0 | D. | x=3 |
 画出下面几何体的从正面、从左面、从上面看到的形状图.
画出下面几何体的从正面、从左面、从上面看到的形状图.