题目内容
 如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于
如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于| 1 |
| 2 |
(1)∠ADE=
(2)AE
(3)当AB=3,AC=5时,△ABE的周长=
考点:线段垂直平分线的性质,勾股定理的应用
专题:几何图形问题
分析:(1)由作图可知,MN是线段AC的垂直平分线,故可得出结论;
(2)根据线段垂直平分线的性质即可得出结论;
(3)先根据勾股定理求出BC的长,进而可得出结论.
(2)根据线段垂直平分线的性质即可得出结论;
(3)先根据勾股定理求出BC的长,进而可得出结论.
解答:解:(1)∵由作图可知,MN是线段AC的垂直平分线,
∴∠ADE=90°.
故答案为:90°;
(2)∵MN是线段AC的垂直平分线,
∴AE=EC.
故答案为:=;
(3)∵在Rt△ABC中,∠B=90°,AB=3,AC=5,
∴BC=
=4,
∵AE=CE,
∴△ABE的周长=AB+BC=3+4=7.
故答案为:7.
∴∠ADE=90°.
故答案为:90°;
(2)∵MN是线段AC的垂直平分线,
∴AE=EC.
故答案为:=;
(3)∵在Rt△ABC中,∠B=90°,AB=3,AC=5,
∴BC=
| 52-33 |
∵AE=CE,
∴△ABE的周长=AB+BC=3+4=7.
故答案为:7.
点评:本题考查的是线段垂直平分线的性质以及勾股定理的应用,熟知线段垂直平分线的性质是解答此题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目

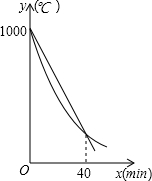 某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB= 已知一次函数y=kx+b经过点B(-1,0),与反比例函数y=
已知一次函数y=kx+b经过点B(-1,0),与反比例函数y=