题目内容
在平面直角坐标系xOy中,射线l:y=
x(x≥0).点A是第一象限内一定点,OA=4
,射线OA与射线l的夹角为30°.射线l上有一动点P从点O出发,以每秒2
个单位长度的速度沿射线l匀速运动,同时x轴上有一动点Q从点O出发,以相同的速度沿x轴正方向匀速运动,设运动时间为t秒.
(1)用含t的代数式表示PQ的长.
(2)若当P、Q运动某一时刻时,点A恰巧在线段PQ上,求出此时的t值.
(3)定义M抛物线:顶点为P,且经过Q点的抛物线叫做“M抛物线”.若当P、Q运动t秒时,将△PQA绕其某边中点旋转180°后,三个对应顶点恰好都落在“M抛物线”上,求此时t的值.
| 3 |
| 3 |
| 3 |
(1)用含t的代数式表示PQ的长.
(2)若当P、Q运动某一时刻时,点A恰巧在线段PQ上,求出此时的t值.
(3)定义M抛物线:顶点为P,且经过Q点的抛物线叫做“M抛物线”.若当P、Q运动t秒时,将△PQA绕其某边中点旋转180°后,三个对应顶点恰好都落在“M抛物线”上,求此时t的值.
考点:二次函数综合题
专题:
分析:(1)根据射线l解析式为y=
x(x≥0)得到∠POQ=60°,利用P,Q运动速度相同,得到OP=OQ=2
t,然后利用△OPQ是等边三角形表示出PQ=2
t;
(2)首先根据题意表示出A(6,2
),P(
t,3t),Q(2
t,0),然后过点A作AB⊥x轴于B,得到AB=2
在Rt△ABQ中,∠ABQ=90°,∠AQB=60°,从而求得BQ,求得OQ的长即可求得时间;
(3)首先由抛物线的对称性得到抛物线经过P、Q、O三点P(
t,3t),Q(2
t,0),O(0,0),设:抛物线M的解析式为y=ax(x-2
t);将P(
t,3t)代入可得a=-
从而确定抛物线的解析式为:y=-
x2+2
x,然后根据对称轴四边形PAQA′是平行四边形,例用P(
t,3t),Q(2
t,0),A(6,2
),得到A′(3
t-6,3t-2
),代入抛物线y=-
x2+2
x即可求得时间t.
| 3 |
| 3 |
| 3 |
(2)首先根据题意表示出A(6,2
| 3 |
| 3 |
| 3 |
| 3 |
(3)首先由抛物线的对称性得到抛物线经过P、Q、O三点P(
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| t |
| 1 |
| t |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| t |
| 3 |
解答:解:(1)∵射线l解析式为y=
x(x≥0),
∴∠POQ=60°.
∵P,Q运动速度相同,
∴OP=OQ=2
t,
∴△OPQ是等边三角形,
∴PQ=2
t;
(2)由题意:A(6,2
),P(
t,3t),Q(2
t,0),
过点A作AB⊥x轴于B,如图1,
则AB=2
,
∵在Rt△ABQ中,∠ABQ=90°,∠AQB=60°,
∴BQ=
=2,

∴OQ=OB+BQ=8,
∴t=
=
秒;
(3)由抛物线的对称性知:抛物线经过P、Q、O三点P(
t,3t),Q(2
t,0),O(0,0), 如图2,
如图2,
不妨设:抛物线M的解析式为y=ax(x-2
t),
将P(
t,3t)代入可得a=-
,
得到抛物线的解析式为:y=-
x2+2
x,
显然:△PQA绕PQ中点旋转180°后,三个对应顶点在抛物线上,
设A的对应点为A′,如图3,
得到四边形PAQA′是平行四边形,
∵P(
t,3t),Q(2
t,0),A(6,2
),
∴A′(3
t-6,3t-2
),
将A′(3
t-6,3t-2
),代入抛物线y=-
x2+2
x,
解得t=
或t=
,
∴当经过t=
秒或t=
秒时,△PQA绕PQ中点旋转180°后,三个对应顶点在“M抛物线”上.
| 3 |
∴∠POQ=60°.
∵P,Q运动速度相同,
∴OP=OQ=2
| 3 |
∴△OPQ是等边三角形,
∴PQ=2
| 3 |
(2)由题意:A(6,2
| 3 |
| 3 |
| 3 |
过点A作AB⊥x轴于B,如图1,
则AB=2
| 3 |
∵在Rt△ABQ中,∠ABQ=90°,∠AQB=60°,
∴BQ=
| AB | ||
|

∴OQ=OB+BQ=8,
∴t=
| OQ | ||
2
|
| 4 |
| 3 |
| 3 |
(3)由抛物线的对称性知:抛物线经过P、Q、O三点P(
| 3 |
| 3 |
 如图2,
如图2,不妨设:抛物线M的解析式为y=ax(x-2
| 3 |
将P(
| 3 |
| 1 |
| t |
得到抛物线的解析式为:y=-
| 1 |
| t |
| 3 |
显然:△PQA绕PQ中点旋转180°后,三个对应顶点在抛物线上,
设A的对应点为A′,如图3,
得到四边形PAQA′是平行四边形,
∵P(
| 3 |
| 3 |
| 3 |
∴A′(3
| 3 |
| 3 |
将A′(3
| 3 |
| 3 |
| 1 |
| t |
| 3 |
解得t=
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |
∴当经过t=
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
| 3 |

点评:本题考查了二次函数的综合知识,题目中涉及到了动点问题,并且与几何知识联系起来,难度较大.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于
如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)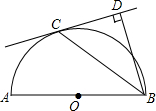 如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA.
如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA.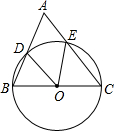 如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE=
如图,以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E,连结OD、OE,若∠A=65°,则∠DOE=