题目内容
 已知一次函数y=kx+b经过点B(-1,0),与反比例函数y=
已知一次函数y=kx+b经过点B(-1,0),与反比例函数y=| k |
| x |
(1)分别求两个函数的关系式;
(2)直线AD经过点A与x轴交于点D,当∠BAD=90°时,求点D的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据待定系数法就可以求出函数的解析式;
(2)由∠BAD=90°,所以直线AD与直线AB垂直,设直线AD的解析式为y=-
x+m,直线AD经过点A(1,4),求得直线AD的解析式,再求点D的坐标即可.
(2)由∠BAD=90°,所以直线AD与直线AB垂直,设直线AD的解析式为y=-
| 1 |
| 2 |
解答:解:(1)∵点A(1,4)在反比例函数图象上
∴k=4
即反比例函数关系式为y=
∵点A(1,4)和B(-1,0)在一次函数y=kx+b的图象上
∴
解得
,
所以一次函数的解析式为:y=2x+2;
(2)∵∠BAD=90°,
∴直线AD与直线AB垂直,
∴设直线AD的解析式为y=-
x+m,
直线AD经过点A(1,4)
∴4=-
+m,
m=
,
∴y=-
x+
,
当y=0时,0=-
x+
,x=9,
∴点D的坐标为(9,0).
∴k=4
即反比例函数关系式为y=
| 4 |
| x |
∵点A(1,4)和B(-1,0)在一次函数y=kx+b的图象上
∴
|
解得
|
所以一次函数的解析式为:y=2x+2;
(2)∵∠BAD=90°,
∴直线AD与直线AB垂直,
∴设直线AD的解析式为y=-
| 1 |
| 2 |
直线AD经过点A(1,4)
∴4=-
| 1 |
| 2 |
m=
| 9 |
| 2 |
∴y=-
| 1 |
| 2 |
| 9 |
| 2 |
当y=0时,0=-
| 1 |
| 2 |
| 9 |
| 2 |
∴点D的坐标为(9,0).
点评:本题主要考查了反比例函数与一次函数的交点问题.用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
下图能说明∠1>∠2的是( )
A、 |
B、 |
C、 |
D、 |
 如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于
如图,在Rt△ABC中,∠B=90°,分别以A、C为圆心,大于 如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.
如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等. 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)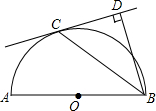 如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA.
如图,已知AB是半圆O的直径,C是半圆O上的一点,BD⊥CD于点D,且BC平分∠DBA.