题目内容
4．
如图，点A在以O为原点的数轴上，OA的长度为3，以OA为直角边，以长度是1的线段AB为另一直角边作Rt△OAB，若以O为圆心，OB为半径作圆，则圆与数轴交点表示的数为（ ）| A． | 3.5 | B． | $\sqrt{10}$ | C． | ±2$\sqrt{2}$ | D． | ±$\sqrt{10}$ |
分析 直接利用勾股定理得出OB的长，再利用数轴得出圆与数轴交点表示的数．
解答 
解：如图所示：OB=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$，
故以O为圆心，OB为半径作圆，则圆与数轴交点表示的数为：±$\sqrt{10}$．
故选：D．
点评 此题主要考查了实数与数轴以及勾股定理，得出BO的长是解题关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
14．三角形的一个外角等于与它不相邻的一个内角的4倍，等于与它相邻的内角的2倍，则该三角形各角的度数为（ ）
| A． | 45、45、90 | B． | 30、60、90 | C． | 25、25、130 | D． | 36、72、72 |
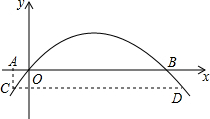如图是某拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可以近似看成抛物线y=-$\frac{1}{400}$（x-80）2+16，桥拱与桥墩AC的交点C恰好在水面，有AC⊥x轴．若OA=10米，则桥面离水面的高度AC为$\frac{17}{4}$米．
如图，以40m/s的速度将小球沿与地面成某一角度的方向击出时，小球的飞行路线将是一条抛物线．如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间（单位：s）之间具有函数关系h=20t-5t2．请解答以下问题：
9．我们用有理数的运算研究下面问题．规定：水位上升为正，水位下降为负；几天后为正，几天前为负．如果水位每天下降4cm，那么3天后的水位变化用算式表示正确的是（ ）
| A． | （+4）×（+3） | B． | （+4）×（-3） | C． | （-4）×（+3） | D． | （-4）×（-3） |