题目内容
17. 如图,在△ABC中,AB=6,BC=9,点D,E分别在边BC,AC上,∠ADE=∠ABC,ED与AB的延长线交于点F.
如图,在△ABC中,AB=6,BC=9,点D,E分别在边BC,AC上,∠ADE=∠ABC,ED与AB的延长线交于点F.(1)求证:△DBF∽△ADF;
(2)当BD=4时,求$\frac{AD}{AC}$的值;
(3)在第(2)题的条件下,若AC=8,求BF的长.
分析 (1)由∠ADE=∠ABC,得到∠ADF=∠DBF 由于∠AFD=∠BFD,于是得到结论;
(2)在△ABC与△ADB中,由于$\frac{AB}{BD}=\frac{6}{4}=\frac{3}{2}$,$\frac{BC}{AB}$=$\frac{9}{6}$=$\frac{3}{2}$,于是得到$\frac{AB}{BD}=\frac{BC}{AB}$,由∠ABD是公共角,于是证得△ABC∽△ADB,即可得到结论;
(3)由(1)知△DBF∽△ADF,根据相似三角形的性质得到$\frac{BF}{DF}=\frac{DF}{AF}$=$\frac{BD}{AD}$,求得$\frac{BF}{DF}=\frac{DF}{AF}$=$\frac{4}{\frac{16}{3}}$=$\frac{3}{4}$,于是得到DF2=BF•AF=BF(BA+BF),列方程即可求得结果.
解答 (1)证明:∵∠ADE=∠ABC,
∴∠ADF=∠DBF
∵∠AFD=∠BFD,
∴△DBF∽△ADF;
(2)∵在△ABC与△ADB中,
∵$\frac{AB}{BD}=\frac{6}{4}=\frac{3}{2}$,$\frac{BC}{AB}$=$\frac{9}{6}$=$\frac{3}{2}$,
∴$\frac{AB}{BD}=\frac{BC}{AB}$,
∵∠ABD是公共角,
∴△ABC∽△ADB,
∴$\frac{AC}{AD}=\frac{AB}{BD}=\frac{3}{2}$;
(3)由(1)知△DBF∽△ADF,
∴$\frac{BF}{DF}=\frac{DF}{AF}$=$\frac{BD}{AD}$,
∵$\frac{AC}{AD}$=$\frac{3}{2}$,AC=8,
∴AD=$\frac{16}{3}$,
∴$\frac{BF}{DF}=\frac{DF}{AF}$=$\frac{4}{\frac{16}{3}}$=$\frac{3}{4}$,
∴DF2=BF•AF=BF(BA+BF),
∴$\frac{DF}{AF}=\frac{\sqrt{BF(AB+BF)}}{AB+BF}$=$\frac{3}{4}$,
∴$\frac{BF}{6+BF}=\frac{9}{16}$,
解得:BF=$\frac{54}{7}$.
点评 本题考查了相似三角形的判定和性质,三角形外角的性质,熟练掌握相似三角形的判定和性质是解题的关键.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案依次划分下

(1)根据题意,完成表格
| 划分次数 | 扇形总个数 |
| 1 | 6 |
| 2 | 11 |
| 3 | 16 |
| 4 | 21 |
| … | … |
| n | 5n+1 |
 如图,在⊙O中,弦AB、CD相交于点E,∠BAC=40°,∠AED=75°,求∠ABD的度数.
如图,在⊙O中,弦AB、CD相交于点E,∠BAC=40°,∠AED=75°,求∠ABD的度数.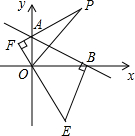 如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点
如图,直线y=-$\frac{1}{2}$x+2与坐标轴于A、B两点,BE⊥AB,BE=AB,AF⊥OE,垂足为F点 如图,在△ABC中,∠C=90°,正方形DEFG内接于△ABC,其中点D、E在边AB上,点F、G分别在边BC,CA上,已知$\frac{AC}{BC}$=k,则AD:DE:EB=k2:k:1(用k表示)
如图,在△ABC中,∠C=90°,正方形DEFG内接于△ABC,其中点D、E在边AB上,点F、G分别在边BC,CA上,已知$\frac{AC}{BC}$=k,则AD:DE:EB=k2:k:1(用k表示)