题目内容
已知函数y=(m+3)xm2+3m-2是关于x的二次函数.
(1)求m的值;
(2)指出该函数图象的开口方向、对称轴及y随x的变化情况.
(1)求m的值;
(2)指出该函数图象的开口方向、对称轴及y随x的变化情况.
考点:二次函数的性质,二次函数的定义
专题:
分析:(1)根据二次函数的定义列出关系式m2+3m-2=2且m+3≠0,求解即可;
(2)根据二次函数的二次项系数判断该函数图象的开口方向,由二次函数的顶点式关系式找出对称轴,由二次函数的单调性来判断它的变化情况.
(2)根据二次函数的二次项系数判断该函数图象的开口方向,由二次函数的顶点式关系式找出对称轴,由二次函数的单调性来判断它的变化情况.
解答:解:(1)∵函数y=(m+3)xm2+3m-2是关于x的二次函数,
∴m2+3m-2=2且m+3≠0,
解得m=1或-4,
∴m=1或-4;
(2)当m=1时,y=4x2,
∵a=4>0,
∴函数图象开口向上,对称轴为y轴,
∴在y轴的左侧,y随x的增大而减小,在y轴的右侧,y随x的增大而增大;
当m=-4时,y=-x2,
∵a=-1<0,
∴函数图象开口向下,对称轴为y轴,
∴在y轴的左侧,y随x的增大而增大,在y轴的右侧,y随x的增大而减小.
∴m2+3m-2=2且m+3≠0,
解得m=1或-4,
∴m=1或-4;
(2)当m=1时,y=4x2,
∵a=4>0,
∴函数图象开口向上,对称轴为y轴,
∴在y轴的左侧,y随x的增大而减小,在y轴的右侧,y随x的增大而增大;
当m=-4时,y=-x2,
∵a=-1<0,
∴函数图象开口向下,对称轴为y轴,
∴在y轴的左侧,y随x的增大而增大,在y轴的右侧,y随x的增大而减小.
点评:本题主要考查的是二次函数的性质及二次函数的定义,是基础知识,需熟练掌握.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
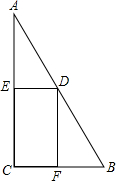 如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )
如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,点D是AB上的一个动点(不与A、B两点重合),DE⊥AC于点E,DF⊥BC于点F,点D从靠近点A的某一点向点B移动,矩形DECF的周长变化情况是( )| A、逐渐减小 |
| B、逐渐增大 |
| C、先增大后减小 |
| D、先减小后增大 |
 作图题:
作图题: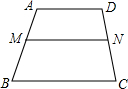 如图,在梯形ABCD中AD∥BC,点M为腰AB上的一点,MN∥BC交DC于点N,MN与AD是否平行?请说明理由,分别测量出点MN到BC的距离,两者有何关系.
如图,在梯形ABCD中AD∥BC,点M为腰AB上的一点,MN∥BC交DC于点N,MN与AD是否平行?请说明理由,分别测量出点MN到BC的距离,两者有何关系.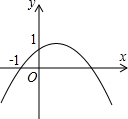 如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>-1时,y>0.其中正确结论的个数是:
如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(-1,0),下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>-1时,y>0.其中正确结论的个数是: