题目内容
正比例函数y=x的图象与反比例函数y=
的图象有一个交点的横坐标是2.
(1)当x=-3时,求反比例函数y=
的值;
(2)当-3<x<-1时,求反比例函数y=
的取值范围.
| k |
| x |
(1)当x=-3时,求反比例函数y=
| k |
| x |
(2)当-3<x<-1时,求反比例函数y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)首先把x=2代入直线的解析式,求得交点坐标,然后利用待定系数法求得反比例函数的解析式,最后把x=-3代入求解;
(2)首先求得当x=-3和x=-1时y的值,然后根据反比例函数的性质求解.
(2)首先求得当x=-3和x=-1时y的值,然后根据反比例函数的性质求解.
解答:解:(1)在y=x中,当x=2时,y=2,则交点坐标是(2,2),
把(2,2)代入y=
,得:k=4,
当x=-3,y=-
;
(2)当x=-3时,y=-
;
当x=-1时,y=-4,
则当当-3<x<-1时,y的范围是:-4<y<-
.
把(2,2)代入y=
| k |
| x |
当x=-3,y=-
| 4 |
| 3 |
(2)当x=-3时,y=-
| 4 |
| 3 |
当x=-1时,y=-4,
则当当-3<x<-1时,y的范围是:-4<y<-
| 4 |
| 3 |
点评:本题考查了待定系数法求函数的解析式以及反比例函数的性质,注意当k>0时,在每个象限内y随x的增大而减小.

练习册系列答案
相关题目
文具店、书店和玩具店依次坐落在一条东西走向的大街上,文具店在书店西边200m处,玩具店位于书店东边100m处,小明从书店沿街向东走了40m,接着又向西走了-60m,这时小明的位置( )
| A、文具店 |
| B、玩具店 |
| C、文具店西边40m |
| D、玩具店东边-60m |
 如图所示,梯形ABCD中,AB∥DC.AD=BC=DC=2,AC⊥BC,求AB,AC的长.
如图所示,梯形ABCD中,AB∥DC.AD=BC=DC=2,AC⊥BC,求AB,AC的长.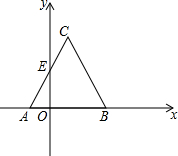 如图所示的平面直角坐标系,在△ABC中,∠A=60°,边AB在x轴上,AC交y轴于点E,AC、BC的长是关于x的方程x2-16x+64=0的两个根,且OA:OB=1:3.
如图所示的平面直角坐标系,在△ABC中,∠A=60°,边AB在x轴上,AC交y轴于点E,AC、BC的长是关于x的方程x2-16x+64=0的两个根,且OA:OB=1:3.