题目内容
2.下列命题:①若a+b+c=0,则b2-4ac≥0;
②若b>a+c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
③若b=2a+3c,则一元二次方程ax2+bx+c=0有两个不相等的实数根;
④若b2-4ac>0,则二次函数的图象与坐标轴的公共点的个数是2或3.
其中正确的是①③④.
分析 ①根据完全平方公式,可得答案;
②根据根的判别式,可得答案;
③根据根的判别式,可得答案;
④根据根的判别式,可的响应的函数图象与坐标轴交点的个数.
解答 解:①由a+b+c=0得b=-a-c,
∴b2-4ac=(-a-c)2-4ac=(a-c)2≥0,故①正确;
②由b>a+c,b2和(a+c)2无法比较,从而无法判断b2-4ac的大小,若b<0,则b2<(a+c)2;若a+c>0,则b2>(a+c)2;故②错误;
③若b=2a+3c,则b2-4ac=4a2+8ac+9c2=4(a+c)2+5c2≥0,则一元二次方程ax2+bx+c=0有两个实数根,又a≠0,则a+c和c必有一个不为0;故判别式△>0;即有两根且不等;故③正确
④若b2-4ac>0,则二次函数的图象与坐标轴的公共点的个数是2或3,故④正确;
故答案为:①③④.
点评 本题考查了命题与定理,利用完全平方公式,根的判别式大于零一元二次方程有两个实数根,相应的二次函数与x轴有两个交点,与y轴有一个交点.判别式等于零一元二次方程有两个相等的实数根.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
17.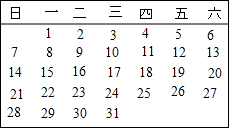 如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )
如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )
 如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )
如图是某月的月历,横着或竖着取连续的三个数字,它们的和可能是( )| A. | 18 | B. | 33 | C. | 38 | D. | 81 |
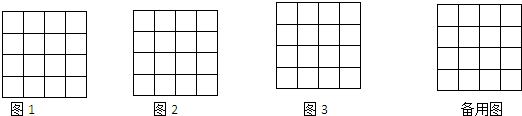
 将如图中几何体的截面用阴影部分表示出来,并分别指出它们的形状.
将如图中几何体的截面用阴影部分表示出来,并分别指出它们的形状.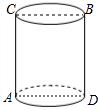 一个无盖圆柱形纸筒的底面周长是60厘米,高是40厘米,如图,一只小蚂蚁在圆筒底部的A处,它想吃到上底面上与点A相对的B点处的蜜糖,
一个无盖圆柱形纸筒的底面周长是60厘米,高是40厘米,如图,一只小蚂蚁在圆筒底部的A处,它想吃到上底面上与点A相对的B点处的蜜糖,