题目内容
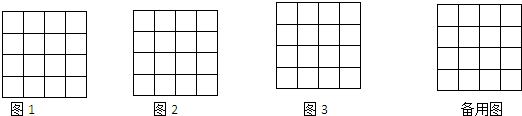
4.如图所示,在大小为4X4的正方形网格中,每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求作答.(1)在图1中,画一条长为$\sqrt{13}$的线段;
(2)在图2中,画一个正方形,使它的面积是8;
(3)在图3中,画一个直角三角形,使它们的三边长都是无理数;
(4)三个顶点都在格点的直角三角形共有17个.(全等的三角形只算一个)
分析 (1)由勾股定理得出$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,画出图形即可;
(2)由勾股定理得出$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,画出正方形即可;
(3)由勾股定理得出$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,由($\sqrt{5}$)2+($\sqrt{5}$)2=($\sqrt{10}$)2,根据勾股定理的逆定理画出图形即可;
(4)斜边长分别为$\sqrt{2}$;2;2$\sqrt{2}$;4;3$\sqrt{2}$;4$\sqrt{2}$;$\sqrt{5}$;$\sqrt{17}$;$\sqrt{13}$;5的直角三角形的个数;斜边长为$\sqrt{10}$和2$\sqrt{5}$的直角三角形的个数;即可得出结果
解答 解:(1) 由勾股定理得:$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
由勾股定理得:$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,
线段如图1所示;
(2)由勾股定理得:$\sqrt{{2}^{2}+{2}^{2}}$=$\sqrt{8}$=2$\sqrt{2}$,
正方形如图2所示;
(3)∵$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
($\sqrt{5}$)2+($\sqrt{5}$)2=($\sqrt{10}$)2,
∴如图3中三角形即为所求;
(4)斜边长分别为$\sqrt{2}$;2;2$\sqrt{2}$;4;3$\sqrt{2}$;4$\sqrt{2}$;$\sqrt{5}$;$\sqrt{17}$;$\sqrt{13}$的直角三角形各1个;斜边为5的直角三角形有2个;
斜边长为$\sqrt{10}$的直角三角形有3个,
斜边长为2$\sqrt{5}$的直角三角形有3个;
∴三个顶点都在格点的直角三角形共有17个;
故答案为:17.
点评 本题考查了正方形的性质、勾股定理、勾股定理的逆定理;熟练掌握正方形的性质,运用勾股定理和勾股定理的逆定理画出图形是解决问题的关键.

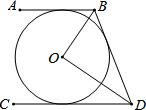 如图,AB、CD、BD都与⊙O相切,AB∥CD,OB=2,OD=3,则BD=$\sqrt{13}$.
如图,AB、CD、BD都与⊙O相切,AB∥CD,OB=2,OD=3,则BD=$\sqrt{13}$.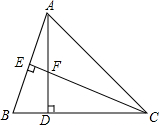 已知△ABC中,AD=CD,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于F点,且AE=$\frac{1}{2}$CF.求证:CE平分∠ACB.
已知△ABC中,AD=CD,AD⊥BC,CE⊥AB,垂足分别为D,E,AD与CE相交于F点,且AE=$\frac{1}{2}$CF.求证:CE平分∠ACB.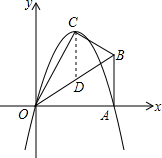 如图,已知点A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2).将△OAB沿OB折叠后,点A落在点c处,抛物线经过O、A、C三点,其对称轴与OB交于点D.
如图,已知点A (2$\sqrt{3}$,0)、B(2$\sqrt{3}$,2).将△OAB沿OB折叠后,点A落在点c处,抛物线经过O、A、C三点,其对称轴与OB交于点D.