题目内容
10. 如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数$\frac{k}{x}$(k≠0)的图象交于A、B两点.与y轴交于点C,过点B作BD⊥y轴于点D.己CD=3,tan∠BCD=$\frac{2}{3}$.点B的坐标为(m,-1).
如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数$\frac{k}{x}$(k≠0)的图象交于A、B两点.与y轴交于点C,过点B作BD⊥y轴于点D.己CD=3,tan∠BCD=$\frac{2}{3}$.点B的坐标为(m,-1).(1)求线段BC的长:
(2)求反比例函数和一次函数的解析式.
分析 (1)在Rt△BCD中,根据正切的定义可得出BD的长度,再根据勾股定理即可得出BC的长度;
(2)由BC的长度结合点B的坐标,即可得出点B及点C的坐标,根据点B、C的坐标,利用待定系数法即可求出一次(反比例)函数解析式.
解答 解:(1)在Rt△BCD中,∠BDC=90°,CD=3,tan∠BCD=$\frac{2}{3}$,
∴BD=2,BC=$\sqrt{C{D}^{2}+B{D}^{2}}$=$\sqrt{13}$.
(2)∵BD=2,点B的坐标为(m,-1),CD=3,
∴m=2,OD=1,OC=2,
∴点B的坐标为(2,-1),点C的坐标为(0,2).
将点B(2,-1)、C(0,2)代入y=ax+b中,
$\left\{\begin{array}{l}{2a+b=-1}\\{b=2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=2}\end{array}\right.$,
∴一次函数的解析式为y=-$\frac{3}{2}$x+2.
将点B(2,-1)代入y=$\frac{k}{x}$中,
-1=$\frac{k}{2}$,解得:k=-2,
∴反比例函数的解析式为y=-$\frac{2}{x}$.
点评 本题考查了解直角三角形、反比例函数与一次函数的交点问题以及待定系数法求一次(反比例)函数解析式,解题的关键是:(1)利用勾股定理求出BC的长度;(2)根据点的坐标,利用待定系数法求出函数解析式.

练习册系列答案
相关题目
5.把-2xy-4x2y+2xy2提取公因式后,另一个因式是( )
| A. | -2-4x+2y | B. | -1-2x+y | C. | 1+2x-y | D. | 2x-y |
15.下列函数中,y随x增大而减小的是( )
| A. | y=$\frac{2}{x}$ | B. | y=$\frac{-2}{x}$ | C. | y=-2x+4 | D. | y=4+2x |
 (1)计算:($\sqrt{3}$-1)0+2sin30°-($\frac{1}{2}$)-1+|-2017|;
(1)计算:($\sqrt{3}$-1)0+2sin30°-($\frac{1}{2}$)-1+|-2017|; 如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.
如图,已知:点A(0,2),动点P从点A出发,沿y轴以每秒1个单位长度的速度向上移动,且过点P的直线l:y=-2x+b也随之移动,并与x轴交于点B,设动点P移动时间为t s.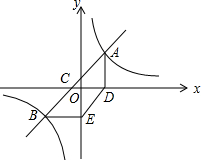 如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E.
如图,已知双曲线y=$\frac{k}{x}$经过点A(3,$\frac{20}{3}$),点B是双曲线第三象限上的一个动点,过点A作AD⊥x轴于点D,过点B作BE⊥y轴于点E. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=2$\sqrt{2}$,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1,矩形PDFE的面积为S2,y=S1+S2,则y与x的关系式是y=-x2+3x.
如图,在Rt△ABC中,∠BAC=90°,AB=AC=2$\sqrt{2}$,AD为BC边上的高,动点P在AD上,从点A出发,沿A→D方向运动,设AP=x,△ABP的面积为S1,矩形PDFE的面积为S2,y=S1+S2,则y与x的关系式是y=-x2+3x.