题目内容
2.若|x+1|+|y-$\frac{1}{2}$|=0,那么x-y=$-\frac{3}{2}$.分析 根据非负数的性质列出方程组求出x、y的值,再代入即可.
解答 解:∵|x+1|+|y-$\frac{1}{2}$|=0,
∴x+1=0,y-$\frac{1}{2}$=0,
∴x=-1,y=$\frac{1}{2}$,
∴x-y=-1$-\frac{1}{2}$=-$\frac{3}{2}$,
故答案为:-$\frac{3}{2}$.
点评 本题考查了代数式求值,利用非负数的性质:几个非负数的和为0时,这几个非负数都为0是解答此题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
11.下列说法正确的是( )
| A. | 点(2,4)在函数y=2x+4的图象上 | |
| B. | 已知甲,乙两组数据的个数相同且平均数相等,若甲组数据的方差S甲2=0.06,乙组数据的方差S乙2=0.105,则甲的波动比乙的波动小 | |
| C. | Rt△ABC的边a=3、b=4,则第三边c=5 | |
| D. | 二元一次方程组$\left\{\begin{array}{l}{x+y=3}\\{2x-3y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |

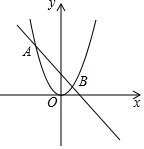 如图,抛物线y=ax2(a≠0)与直线y=bx+c(b≠0)的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx-c=0的解为-2或1.
如图,抛物线y=ax2(a≠0)与直线y=bx+c(b≠0)的两个交点坐标分别为A(-2,4),B(1,1),则关于x的方程ax2-bx-c=0的解为-2或1. 如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为110°.
如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为110°. 已知:△ABC.
已知:△ABC.