题目内容
20. 如图,AB是半圆O的直径,C是半圆上一点.以O为圆心,OE长为半径的半圆交AB于E、F两点,D是其上一动点(可以与E、F两点重合),CD是小半圆的切线,D为切点.已知AO=4,EO=2,设阴影部分的面积为S,则S的取值范围是2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.
如图,AB是半圆O的直径,C是半圆上一点.以O为圆心,OE长为半径的半圆交AB于E、F两点,D是其上一动点(可以与E、F两点重合),CD是小半圆的切线,D为切点.已知AO=4,EO=2,设阴影部分的面积为S,则S的取值范围是2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.
分析 先确定S最大和最小时,C的位置,C的位置确定,则D有唯一的位置对应;①当C与B重合时,如图1,此时S最小;②当C与A重合时,如图2,此时S最大,根据面积差求出即可.
解答  解:连接OD,
解:连接OD,
∵DC为⊙O的切线,
∴OD⊥DC,
∴∠ODC=90°,
①当C与B重合时,如图1,
Rt△ODB中,OD=2,OB=4,
∴DC=2$\sqrt{3}$,
∴∠DOB=60°,
∴S=S△ODB-S扇形ODF=$\frac{1}{2}$×2×2$\sqrt{3}$-$\frac{60π×{2}^{2}}{360}$=2$\sqrt{3}$-$\frac{2π}{3}$;
②当C与A重合时,如图2,
∴S=$\frac{1}{2}$(π•42-π•22)-(2$\sqrt{3}$-$\frac{2π}{3}$),
=6π-2$\sqrt{3}$+$\frac{2π}{3}$,
=$\frac{20π}{3}$-2$\sqrt{3}$;
综上所述,S的取值范围是:2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.
故答案为:2$\sqrt{3}$-$\frac{2π}{3}$≤S≤$\frac{20π}{3}$-2$\sqrt{3}$.
点评 本题考查了切线的性质、扇形面积及阴影面积的求法,利用数形结合的思想,并与切线的性质相联系,确定点C的位置是关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
9.点P(a+b,2a-b)与点Q(-2,-3)关于y轴对称,则a+b的值是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | -2 | D. | 2 |

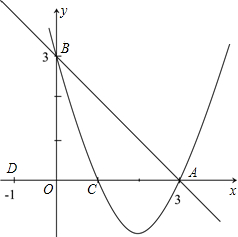 如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.
如图,已知C点的坐标为(1,0),直线y=-x+3交于x轴于点A,交y轴于点B,抛物线y=ax2+bx+c经过A,B,C三点.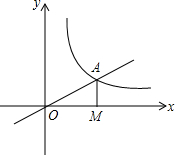 如图所示,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为M,已知△OAM的面积为1.
如图所示,正比例函数y=$\frac{1}{2}$x的图象与反比例函数y=$\frac{k}{x}$(k≠0)在第一象限的图象交于点A,过点A作x轴的垂线,垂足为M,已知△OAM的面积为1.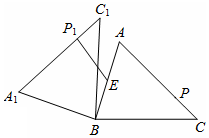 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B旋转,得到△A1BC1.如图,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B旋转过程中,点P的对应点是点P1,线段EP1长度的取值范围为$\frac{{5\sqrt{2}}}{2}-2≤E{P_1}≤7$.
在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B旋转,得到△A1BC1.如图,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B旋转过程中,点P的对应点是点P1,线段EP1长度的取值范围为$\frac{{5\sqrt{2}}}{2}-2≤E{P_1}≤7$.