题目内容
设抛物线y=2x2+kx+1-2k(k为常数)与x轴交于点A、B,与y轴交于点C,并且A点在原点O的左侧,B在原点O的右侧,且(OA+OB)2-OC=
.求:在抛物线上是否存在D、E两点,使AO恰好为△ADE的中线?若存在,求出△ADE的面积;若不存在,说明理由.
| 29 |
| 4 |
考点:抛物线与x轴的交点
专题:
分析:先根据交点和系数的关系,求得k的值,得出解析式,求出A的坐标,得出OA的长,在抛物线上是否存在D、E两点,使AO恰好为△ADE的中线,则D、E是中心对称点,设D(-a,b),则E(a,-b),联立方程求得D的坐标,即可求得△ADE的面积.
解答:解:存在;
设点A(x1,0)、B(x2,0),
由抛物线y=2x2+kx+1-2k(k为常数)可知,x1+x2=-
,x1x2=
,开口向上,交于y轴的负半轴,
∴OA+OB=|x1-x2|,OC=2k-1,
∵(OA+OB)2-OC=
.
∴(OA+OB)2-OC=(x1+x2)2-4x1x2-(2k-1)=
,
即(-
)2-4(
)-(2k-1)=
.解得,k=3或k=-11(不合题意舍去),
∴k=3,
∴抛物线为y=2x2+3x-5,
∴A(-
,0),B(1,0),
∵AO恰好为△ADE的中线,
∴D、E是中心对称点,
∴设D(-a,b),则E(a,-b),
代入y=2x2+3x-5,得
,
解得
或
,
∴D(-
,
),E(
,-
),
∴△ADE的面积=2×
OA•
=
×
=
.
设点A(x1,0)、B(x2,0),
由抛物线y=2x2+kx+1-2k(k为常数)可知,x1+x2=-
| k |
| 2 |
| 1-2k |
| 2 |
∴OA+OB=|x1-x2|,OC=2k-1,
∵(OA+OB)2-OC=
| 29 |
| 4 |
∴(OA+OB)2-OC=(x1+x2)2-4x1x2-(2k-1)=
| 29 |
| 4 |
即(-
| k |
| 2 |
| 1-2k |
| 2 |
| 29 |
| 4 |
∴k=3,
∴抛物线为y=2x2+3x-5,
∴A(-
| 5 |
| 2 |
∵AO恰好为△ADE的中线,
∴D、E是中心对称点,
∴设D(-a,b),则E(a,-b),
代入y=2x2+3x-5,得
|
解得
|
|
∴D(-
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
3
| ||
| 2 |
∴△ADE的面积=2×
| 1 |
| 2 |
3
| ||
| 2 |
| 5 |
| 2 |
3
| ||
| 2 |
15
| ||
| 4 |
点评:本题考查了抛物线和x轴的交点问题,抛物线上点的坐标的特征,D、E是中心对称点,是本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
等腰三角形的一个角是80°,则它的底角度数为( )
| A、50° | B、80° |
| C、80°或50° | D、不确定 |
 如图所示,在形状为平行四边形的一块地中,有一条小路EFG,现在想把它改为过点G的直路,要求小路两侧土地面积都不变,请在图中画出改动后的小路.
如图所示,在形状为平行四边形的一块地中,有一条小路EFG,现在想把它改为过点G的直路,要求小路两侧土地面积都不变,请在图中画出改动后的小路.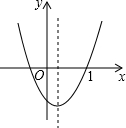 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则c、△(△=b2-4ac)与零的大小关系是c
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则c、△(△=b2-4ac)与零的大小关系是c