题目内容
6.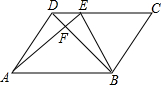 在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF=1:4:16.
在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF=1:4:16.
分析 由DE:EC=1:3得DE:DC=1:4,再根据平行四边形的性质得DC=AB,DC∥AB,则DE:AB=1:4,接着可证明△DEF∽△BAF,根据相似的性质得∴$\frac{DF}{BF}$=$\frac{DE}{AB}$=$\frac{1}{4}$,根据三角形面积公式可得$\frac{{S}_{△DEF}}{{S}_{△EBF}}$=$\frac{1}{4}$,根据相似三角形的性质可得$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{1}{4}$)2,于是可得S△DEF:S△EBF:S△ABF的值.
解答 解:∵DE:EC=1:3,
∴DE:DC=1:4,
∵四边形ABCD为平行四边形,
∴DC=AB,DC∥AB,
∴DE:AB=1:4,
∵DE∥AB,
∴△DEF∽△BAF,
∴$\frac{DF}{BF}$=$\frac{DE}{AB}$=$\frac{1}{4}$,
∴$\frac{{S}_{△DEF}}{{S}_{△EBF}}$=$\frac{DF}{BF}$=$\frac{1}{4}$,$\frac{{S}_{△DEF}}{{S}_{△ABF}}$=($\frac{1}{4}$)2=$\frac{1}{16}$,
∴S△DEF:S△EBF:S△ABF=1:4:16.
点评 本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;在利用三角形相似的性质时,通过相似比计算相应边的长.也考查了平行四边形的性质.

练习册系列答案
相关题目
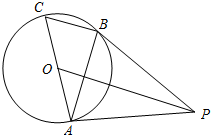 如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.
如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PB、AB,∠PBA=∠C.

 如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD.
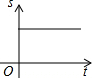
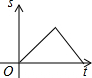
如图,直线AB与CD相交于点O,OE平分∠AOD,OF平分∠BOD. 如图,AB是半圆O的直径,点P从点O出发,沿OA→$\widehat{AB}$→BO的路径运动一周,设点P到点O的距离为S,运动时间为t,则下列图形能大致地刻画S与t之间的关系的是( )
如图,AB是半圆O的直径,点P从点O出发,沿OA→$\widehat{AB}$→BO的路径运动一周,设点P到点O的距离为S,运动时间为t,则下列图形能大致地刻画S与t之间的关系的是( )