题目内容
20.直线AB与CD交于O,OE⊥CD,OF⊥AB,∠DOF=65°,则∠BOE的度数65°或115°.分析 根据题意,分两种情况:(1)∠BOE是锐角时;(2)∠BOE是钝角时;然后根据垂线的性质,分类讨论,求出∠BOE的度数是多少即可.
解答 解:(1)如图1,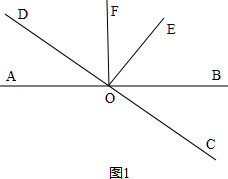 ,
,
∵直线OE⊥CD,
∴∠EOD=90°,
∵∠DOF=65°,
∴∠EOF=90°-65°=25°,
又∵直线OF⊥AB,
∴∠BOF=90°,
∴∠BOE=90°-25°=65°.
(2)如图2,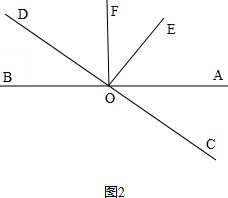 ,
,
∵直线OE⊥CD,
∴∠EOD=90°,
∵∠DOF=65°,
∴∠EOF=90°-65°=25°,
又∵直线OF⊥AB,
∴∠BOF=90°,
∴∠BOE=90°+25°=115°.
综上,可得∠BOE的度数是65°或115°.
故答案为:65°或115°.
点评 (1)此题主要考查了垂线的性质和应用,要熟练掌握,解答此题的关键是要明确:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
(2)此题还考查了对顶角和邻补角的特征和应用,要熟练掌握,解答此题的关键是要明确:①有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角.②补角互补,即和为180°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 由五个小正方体搭成的一个几何体如图所示,它的俯视图是( )
由五个小正方体搭成的一个几何体如图所示,它的俯视图是( )
 由五个小正方体搭成的一个几何体如图所示,它的俯视图是( )
由五个小正方体搭成的一个几何体如图所示,它的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
15.下列说法正确的是( )
| A. | 若ab=0,则点P(a,b)表示原点 | |
| B. | 点(1,-a2)在第四象限 | |
| C. | 已知点A(2,3)与点B(2,-3),则直线AB平行x轴 | |
| D. | 坐标轴上的点不属于任何象限 |
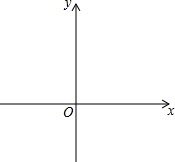 已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.
已知点O(0,0),B(2,3),点A在坐标轴上,且S△AOB=6.