题目内容
1.下面式子是二次根式的是( )| A. | $\sqrt{{a}^{2}+1}$ | B. | $\root{3}{33}$ | C. | $\sqrt{-1}$ | D. | $\frac{1}{2}$a |
分析 直接利用二次根式定义分析得出答案.
解答 解:A、$\sqrt{{a}^{2}+1}$,∵a2+1>0,∴是二次根式,符合题意;
B、$\root{3}{33}$,是三次根式,不合题意;
C、$\sqrt{-1}$,无意义,不合题意;
D、$\frac{1}{2}$a是整式,不合题意.
故选:A.
点评 此题主要考查了二次根式的定义,正确把握二次根式的定义是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知a+b=5,ab=4,则a-b的值为( )
| A. | 9 | B. | 3 | C. | -3 | D. | ±3 |
12.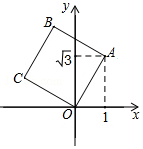 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )
 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )
如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,$\sqrt{3}$),则点B的坐标为( )| A. | (1-$\sqrt{3}$,$\sqrt{3}$+1) | B. | (-$\sqrt{3}$,$\sqrt{3}$+1) | C. | (-1,$\sqrt{3}$+1) | D. | (-1,$\sqrt{3}$) |
9.如果a+b=$\frac{1}{2}$,那么$\frac{a^2}{a-b}+\frac{b^2}{b-a}$的值是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
16.在平面直角坐标系内,将△ABC进行平移后得到△A′B′C′,其中点A(2,1)的对应点A′为(-2,-1),那么△ABC是( )
| A. | 向右平移了4个单位长度 | B. | 向左平移了4个单位长度 | ||
| C. | 向上平移了4个单位长度 | D. | 向下平移了4个单位长度 |
10.某品牌网上专卖店1月份的营业额为50万元,已知第一季度的总营业额共600万元,如果平均每月增长率为x,则由题意列方程应为( )
| A. | 50(1+x)2=600 | B. | 50[1+(1+x)+(1+x)2]=600 | ||
| C. | 50+50×3x=600 | D. | 50+50×2x=600 |
11.在平面直角坐标系中,若一图形各点的纵坐标不变,横坐标分别减5,那么图形与原图形相比( )
| A. | 向右平移了5个单位长度 | B. | 向左平移了5个单位长度 | ||
| C. | 向上平移了5个单位长度 | D. | 向下平移了5个单位长度 |



