题目内容
14.在△ABC中,E、F分别为AB,AC的中点,则△AEF与△ABC的面积之比为1:4.分析 根据三角形的中位线得出EF=$\frac{1}{2}$BC,DE∥BC,推出△EF∽△ABC,根据相似三角形的性质得出即可.
解答 解:∵E、F分别为AB、AC的中点,
∴EF=$\frac{1}{2}$BC,DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=($\frac{EF}{BC}$)2=$\frac{1}{4}$,
故答案为:1:4.
点评 本题考查了三角形的性质和判定,三角形的中位线的应用,注意:相似三角形的面积比等于相似比的平方.

练习册系列答案
相关题目
2.下列各式中正确的是( )
| A. | $\overrightarrow{a}$+(-$\overrightarrow{a}$)=0 | B. | $\overrightarrow{a}$+$\overrightarrow{0}$=-$\overrightarrow{a}$ | C. | $\overrightarrow{0}$+(-$\overrightarrow{a}$)=$\overrightarrow{a}$ | D. | |$\overrightarrow{0}$|=0 |
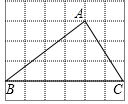 如图,网格图中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则cosB=$\frac{4}{5}$.
如图,网格图中的每个小正方形的边长都是1,△ABC每个顶点都在格点上,则cosB=$\frac{4}{5}$.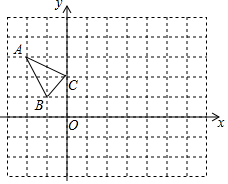 已知△ABC在平面直角坐标系xOy中的位置如图所示.
已知△ABC在平面直角坐标系xOy中的位置如图所示.