题目内容
9．设直线y=kx与双曲线y=$\frac{m}{x}$相交于A（x1，y1）、B（x2，y2）两点，求（x1+x2）（y1+y2）的值．分析 根据A（x1，y1）、B（x2，y2）两点关于原点对称，可得x1+x2=0，y1+y2=0，进而得出（x1+x2）（y1+y2）的值．
解答 解：∵直线y=kx与双曲线y=$\frac{m}{x}$相交于A（x1，y1）、B（x2，y2）两点，
∴A（x1，y1）、B（x2，y2）两点关于原点对称，
∴x1+x2=0，y1+y2=0，
∴（x1+x2）（y1+y2）=0．
点评 本题主要考查了反比例函数与一次函数交点问题，解决问题的关键是利用A（x1，y1）、B（x2，y2）两点关于原点对称对称结论．
练习册系列答案
相关题目
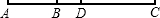如图，已知线段AB=8，延长线段AB到C，使BC=2AB，点D是AC的中点．
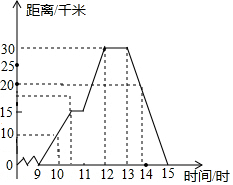如图表示一人骑自行车离家的距离与时间的关系，骑车者9时离开家，15时到家，根据图象回答问题：
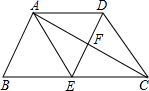四边形ABCD中，AD∥BC，DE⊥AC，∠BAC=90°，E是BC的中点，四边形AECD是菱形．