题目内容
如果一个人的上身长度和下身长度的比满足黄金分割,这个人就会很好看,一个女士的上身为65厘米,下身为97厘米,那么她应该穿多高的高跟鞋才最好看?
考点:黄金分割
专题:计算题
分析:设她应该穿xcm高的高跟鞋才最好看,根据黄金分割的定义得到
=
,然后解方程即可.
| 65 |
| 97+x |
| ||
| 2 |
解答:解:设她应该穿xcm高的高跟鞋才最好看,
根号题意得
=
,
解得x≈8.2(cm).
答:她应该穿8.2cm高的高跟鞋才最好看.
根号题意得
| 65 |
| 97+x |
| ||
| 2 |
解得x≈8.2(cm).
答:她应该穿8.2cm高的高跟鞋才最好看.
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
相关题目
已知二次函数y=(2x-1)2-2,其顶点坐标是( )
| A、(1,-2) | ||
B、(
| ||
C、(-
| ||
| D、(-1,-2) |
下列各组数中,都是无理数的一组是( )
A、-
| |||||
B、
| |||||
C、
| |||||
D、
|
下列计算正确的是( )
| A、2a5+a5=3a10 |
| B、a10÷a2=a8 |
| C、(a2)3=a5 |
| D、a2•a3=a6 |
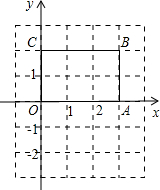 如图,在长方形OABC中,O为平面直角坐标系的原点,A,C的坐标分别为(3,0)、C(0,2),点B在第一象限.
如图,在长方形OABC中,O为平面直角坐标系的原点,A,C的坐标分别为(3,0)、C(0,2),点B在第一象限.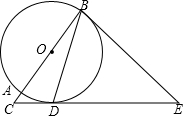 如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.
如图,AB为⊙O的直径,C为BA的延长线上一点,D为⊙O上一点,且∠CDA=∠CBD.