题目内容

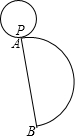如图是一个圆锥的表面展开图，其中小圆是圆锥的底面，点A，B是半圆直径的两个端点，开始时小圆上的点P与A重合，当这个小圆紧贴半圆滚动1周后，你会发现什么现象？由此，你发现半圆的直径与小圆的半径有什么关系．
考点：圆锥的计算
专题：计算题
分析：根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长即可得到当这个小圆紧贴半圆滚动1周后，小圆上的点P与B重合，然后利用弧长公式求出半圆的直径与小圆的半径的关系．
解答：解：当这个小圆紧贴半圆滚动1周后，小圆上的点P与B重合．
设半圆的半径为R，⊙P的半径为r，
则2πr=
180•π•R
180
，
解得R=2r，
所以AB=4r，
所以半圆的直径是小圆的半径的4倍．
点评：本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
相关题目
计算：
（1）（
5
12
-2
3
）×
15

（2）
27
+
3
3
-
6
×
3
2

（3）（
48
-4
1
8
）-（3
1
3
-2
0.5
）
（4）（7+4
3
）（2-
3
）2+（2+
3
）（2-
3
）-
3
．
下列各组数中，都是无理数的一组是（　　）
A、-
2
，
38
B、
22
7
，
π
3
C、
15
，
1000
D、
34
，0
下列计算正确的是（　　）
A、2a5+a5=3a10
B、a10÷a2=a8
C、（a2）3=a5
D、a2•a3=a6
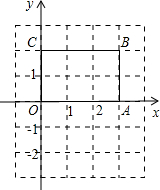如图，在长方形OABC中，O为平面直角坐标系的原点，A，C的坐标分别为（3，0）、C（0，2），点B在第一象限．
（1）写出点B的坐标；
（2）若过点C的直线交长方形的OA边于点D，且把长方形OABC的周长分成2：3的两部分，求点D的坐标；
（3）如果将（2）中的线段CD向下平移3个单位长度，得到对应线段C′D′，在平面直角坐标系中画出△CD′C′，并求出它的面积；
（4）在坐标轴上是否存在点P，使S△CDP的面积为16？如果存在，直接写出点P的坐标；如果不存在，请说明理由．
已知a=
3
4
，b=
4
3
，求（a2-b2）2-（a2+b2）的值．
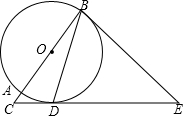如图，AB为⊙O的直径，C为BA的延长线上一点，D为⊙O上一点，且∠CDA=∠CBD．
（1）求证：CD是⊙O的切线；
（2）过点B作⊙O的切线交CD的延长线于点E，若tan∠ADC=
1
2
，求sin∠E的值．
如图所示，在一副三角板ABC和三角板DEC中，∠ACB=∠CDE=90°，∠BAC=60°，∠DEC=45°．
（1）当AB∥DC时，如图①，求∠DCB的度数；
（2）当CD与CB重合时，如图②，判断DE与AC的位置关系，并说明理由；
（3）如图③，当∠DCB等于多少度时，AB∥EC？
（4）当AB∥ED时，如图④⑤，分别求∠DCB的度数．
在数轴上，点A表示的数为4，点B表示的数为-2，则AB两点之间的距离为（　　）
A、-6B、2C、-2D、6

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网